Моделирование статистического прогнозирования. Метод наименьшихквадратов.

На прошлом уроке мы с вами выяснили, что моделирование, да и любое другое исследование начинают с выделения основных количественных характеристик исследуемого объекта, то есть величин.

Понятие величина включает три свойства: имя, значение, тип.

Математической моделью называется совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности изучаемого объекта, процесса или явления.

Отображать зависимости между величинами можно: математически с помощью формулы, таблично и графически.

Информационные модели, описывающие объекты, явления, процессы в определённый момент времени, без учёта их изменений в пространстве и времени, называются статическими.

Такими моделями являются, например, структура кристаллов, классификация растений или животных.

Динамические модели учитывают изменения параметров процессов и явлений с течением времени.

Примером динамической модели является равномерное прямолинейное движение тела.

Также на прошлом уроке мы выяснили, что существуют различные способы представления зависимостей. То есть зависимость может быть математическая, табличная и графическая.

В свой черёд зависимости могут быть полностью определёнными (помните, мы рассматривали зависимость пути от скорости и зависимость силы тока от напряжения) и более сложные, то есть зависимости, в которых существует влияние других факторов.

Как вы помните на прошлом уроке мы не смогли установить зависимость уровня заболеваемости жителей города бронхиальной астмой от качества воздуха. Но оставить нерешённую задачу мы не можем, поэтому сегодня на уроке мы с вами разберёмся со следующими вопросами:

·                   Какая наука называется статистикой, и какие данные называются статистическими;

·                   Для чего используется метод наименьших квадратов;

·                   А также выясним, каким способом можно найти зависимость уровня заболеваемости жителей города бронхиальной астмой от качества воздуха.

Каждому человеку понятно, без лишних доказательств, что чем хуже воздух, тем больше будет больных бронхиальной астмой. Но это общее мнение и на регулирование уровнем загрязнённости воздуха оно никак не влияет.

Для того чтобы в городе начали принимать меры по устранению загрязнённости, необходимы более конкретные данные.

Для начала нужно установить, какие именно примеси сильнее всего влияют на здоровье людей. Затем, как связана концентрация этих примесей в воздухе с числом заболеваний.

Найти такую зависимость можно только экспериментально.

Начинают наблюдать и собирать сведения, затем анализировать их и делать выводы.

Решением таких задач занимается статистика.

Статистика – это наука, в которой изучаются общие вопросы сбора, измерения и анализа массовых количественных или качественных данных.

Статистикой занимаются в разных научных областях. Это и математическая статистика, экономическая статистика, социальная статистика и другие виды.  На этом уроке мы рассмотрим пример медицинской статистики.

По данным исследований известно, что самое большое влияние на бронхиально-лёгочные заболевания оказывает угарный газ.

Работники медицинской статистики начинаю проводить сбор данных. В разных городах берут пробы воздуха, устанавливают концентрацию в нём угарного газа и сравнивают с числом хронических больных бронхиальной астмой на 1000 жителей города.

Полученные данные заносят в таблицу и строят диаграммы.

По статистическим данным нельзя достоверно сказать, например, сколько больных астмой в городе. Так как они приближенные или ещё говорят усреднённые. Статистические данные носят оценочный характер, то есть они проверяют уровень зависимости и правильно показывают её вид.

Также важно отметить, чтобы получить более точный результат, статистических данных должно быть много.

Рассмотрим таблицу, в которую внесены статистические данные, собранные в нескольких городах. Здесь, в учебных целях, мы не будем брать много статистических данных. Для наглядности примера нам будет достаточно десяти таких данных. И построим график по данной таблице.

Теперь по данным из таблицы, а также по графику можно сделать вывод, что при концентрации угарного газа до 3 миллиграмм на метр кубический его влияние на заболеваемость астмой слабое. Но с ростом концентрации угарного газа наступает и резкий рост заболеваемости астмой.

Теперь нам нужно построить математическую модель данного явления.

Напомним, математической моделью называется совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности изучаемого объекта, процесса или явления.

Получается, для построения математической модели нам нужно формула, которая будет показывать зависимость по данным собранным медицинскими статистами.

Напомним: концентрацию примесей мы обозначили буквой C и его единица измерения миллиграмм на метр кубический. Уровень заболеваемости обозначили буквой P, измеряется в больных на тысячу.

Иначе говоря, нам нужно получить функцию P от C. Но такой функции нет и получить её мы можем только методом подбора по экспериментальным данным.

Для начала отметим, что график функции, который нам нужно получить должен проходить близко к точкам диаграммы. Необходимости в том, чтобы координаты графика точно совпадали с точками диаграммы, нет. Так, как и формула может получиться сложной, да и точности не нужно (мы уже говорили, что статистические данные являются приближёнными).

То есть для получения функции нужно соблюдать правила:

Первое: функция должны быть простой, так как она будет применяться в следующих вычислениях.

И второе: график должен проходить вблизи экспериментальных точек с минимальным отклонением.

Полученную таким образом функцию в статистике называют регрессионной моделью.

Регрессионная модель – это функция, описывающая зависимость между количественными характеристиками сложных систем.

Для получения регрессионной модели нужно сначала подобрать вид функции, затем вычислить параметры функции.

Для того чтобы подобрать вид функции чаще всего рассматривают стандартные функций:

·                   линейную;

·                   квадратичную;

·                   логарифмическую;

·                   экспоненциальную.

Нужно внимательно посмотреть на диаграмму. Определить, на график какой из предложенных функций больше всего похожа линия диаграммы. 

Из уроков математики вы знаете, что во всех формулах используют следующие обозначения. x — это аргумент, y — значение функции, а a, b и c — коэффициенты функции, также используются обозначения для натурального логарифма и для постоянного значения основания натурального логарифма.

Итак, больше всего нам подходят графики линейной функции, одной ветви квадратичной функции и экспоненциальной функции. Оставим пока все три варианта.

На следующем этапе получения регрессионной модели нужно вычислить параметры функции. Подобрать коэффициенты для функции. Причём коэффициенты должны быть такими, чтобы полученный график функции располагался как можно ближе к экспериментальным точкам.

Подберём коэффициенты с помощью метода наименьших квадратов (или сокращённо МНК), который был предложен в 18 веке немецким математиком Карлом Фридрихом Гауссом.

По данному методу искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.

Метод наименьших квадратов часто используется в статистике и встроен во многие математические программы.  Но мы не будем рассматривать его подробно. Главное нужно понять: методом наименьших квадратов по данному набору экспериментальных точек можно построить любую функцию.

Здесь, для построения графиков использовался табличный процессор Microsoft Excel.

Полученный таким образом график регрессионной модели называется трендом.

Английское слово trend можно перевести как «общее направление» или «тенденция».

Даже по первому взгляду понятно, что линейный тренд не подходит. Как вы помните график линейной функции — это прямая. Полученная по Методу Наименьших Квадратов прямая отражает факт роста заболеваемости от концентрации угарного газа, но по этому графику трудно что-либо сказать о характере этого роста. А вот квадратичный и экспоненциальный тренды правдоподобны.

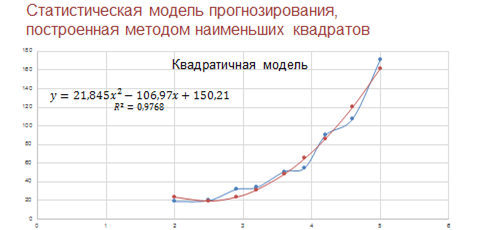
Остановимся подробнее на надписях, присутствующих на графиках. Здесь записаны искомые формулы математической модели или регрессионные модели:

·                   линейной функции;

·                   экспоненциальной функции;

·                   квадратичной функции.

Обратите внимание! На графиках присутствует ещё одна величина, полученная в результате построения трендов, обозначенная как R².

В статистике эта величина называется коэффициентом детерминированности.

Коэффициент детерминированности показывает, насколько удачной является полученная регрессионная модель.

R² всегда заключён в диапазоне от 0 до 1 (Здесь и далее читать единица в нужном склонении). Если он равен 1, то функция точно проходит через табличные значения, т.е. мы получили хорошую модель.

Чем R² ближе к 1, тем удачнее считается регрессионная модель.

Если коэффициент детерминированности равен 0, то выбранный вид регрессионной модели неправильный, т.е. модель плохая.

Как вы видите, из трёх выбранных моделей значение R² наименьшее у линейной, т.е. она самая неудачная (что мы и выяснили ранее).

У двух других моделей значения R² достаточно близки. Значит, обе эти модели одинаково удачны.  Поэтому, для того чтобы выбрать один график, необходимо рассмотреть другие характеристики. Например, если считать, что наиболее существенно влияние концентрации угарного газа проявляется при больших величинах, то, глядя на графики, понятно, что квадратичная модель подходит нам больше. Она лучше отражает резкий рост заболеваемости при больших концентрациях примеси.

То есть мы с вами получили статистическую модель прогнозирования. И построили её методом наименьших квадратов.

А сейчас давайте вспомним, что мы изучили сегодня на уроке:

Статистика – это наука в которой изучаются общие вопросы сбора, измерения и анализа массовых количественных или качественных данных.

Статистические данные – это совокупность объектов (наблюдений, случаев) и признаков (переменных), их характеризующих.

Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.