Моделирование зависимостей между величинами

На прошлом уроке мы с вами начали изучение раздела «Информационное моделирование» и ознакомились с основными понятиями этого раздела.

Мы выяснили, что модель — это объект-заменитель, который в определённых условиях может заменять объект-оригинал. Модель воспроизводит интересующие нас свойства и характеристики оригинала.

Информатика занимается общими методами и средствами создания и использования информационных моделей.

К основным этапам компьютерного моделирования относятся:

Первый этап – Постановка задачи: описание объекта и определение цели моделирования.

Второй этап – Разработка плана создания модели. Выделение свойств объекта, существенных для данной задачи, и отбрасывание второстепенных. Выбор формы представления модели и необходимого инструментария.

Третий этап – Создание модели: формализация, т. е. переход к математической модели; создание алгоритма и написание программы.

Четвёртый этап – Анализ модели на соответствие объекту-оригиналу.

Как мы уже выяснили процесс создания, и использования моделей для решения практических задач называют моделированием.

Моделирование широко используется в науке и технике, экономике и образовании. Без моделирования немыслимо создание машин и механизмов, строительство зданий и мостов, создание новых материалов, лекарств, торговых сетей.

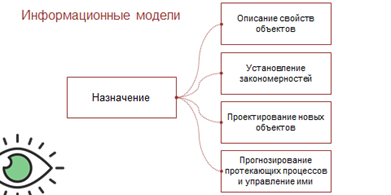
Использование моделей позволяет упростить и удешевить исследование объектов и явлений реального мира. Основное назначение информационных моделей — это описание свойств объектов, установление закономерностей, проектирование новых объектов, прогнозирование протекающих процессов и эффективное управление ими.

Мы с вами будем изучать компьютерное математическое моделирование.

Формальные информационные модели содержат математические и химические формулы, алгоритмы, представленные на языках программирования, и т. д. Например, формулы математики описывают соотношения между количественными характеристиками объекта моделирования.

Применение математического моделирования постоянно требует учёта зависимостей одних величин от других.

Сегодня на уроке мы узнаем:

·                   Что такое величина, и какие существуют формы представления зависимостей.

·                   Что такое математическая модель.

·                   Какие модели называются табличными и графическими.

С зависимостями между величинами вы встречаетесь постоянно на уроках физики и математики. Зависимость может быть прямой и обратной.

Давайте рассмотрим примеры зависимостей:

·                   Пройденный пешеходом путь, за определённый промежуток времени зависит от его скорости;

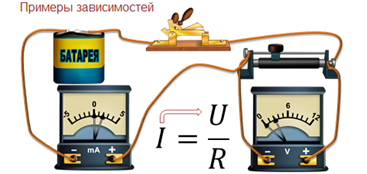
·                   Сила тока на участке цепи зависит от напряжения;

·                   Уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе.

Рассмотрим способы представления зависимостей.

Как вы помните моделирование, да и любое другое исследование начинают с выделения основных количественных характеристик исследуемого объекта, то есть величин.

Понятие величина включает три свойства: имя, значение, тип.

Рассмотрим каждое свойство более подробно.

Итак, имя. Имя величины может быть смысловым или символическим. Например, смысловым именем является «скорость движения», а символическим именем для этой величины будет V.

Имена в языках программирования принято называть идентификаторами. Есть идентификаторы переменных, констант, типов, функций и т.д.

В физике, химии и других науках, которые используют математический аппарат, применяются символические имена для обозначения величин. В основном используют стандартные имена. Например, давление обозначают буквой Р, температуру буквой t.

Следующее свойство величины – это её значение. По значению величины делятся на две группы. К первой группе относятся величины, значения которых не изменяется. Такие величины называются постоянными или константами. Ко второй группе относятся величины, значения которых меняются. Такие величины называются переменными.

Например, константой является скорость света, которая равна 3 умноженное на десять в пятой степени километров в секунду.

Если рассматривать переменные величины, то, например, при равномерном прямолинейном движении тела переменными являются время и путь, а вот скорость будет постоянной.

Третье свойство величины – это её тип. С данным понятием вы также знакомы. Вы встречались с ним при изучении программирования, баз данных, табличных процессоров.

Тип величины определяет диапазон допустимых значений, принимаемых величинами. К основным типам величин относятся: числовой, символьный, логический.

Так как при изучении моделирования нас интересуют только количественные характеристики, то рассматривать мы будем только величины числового типа.

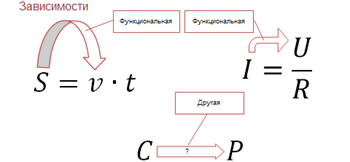
Вернёмся к примерам зависимостей, которые мы рассматривали в начале урока. Обозначим все эти величины и укажем их размерности, то есть укажем единицы, в которых данные величины измеряются.

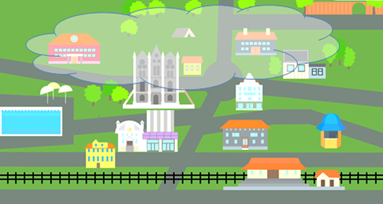
Итак, первый пример. Пройденный пешеходом путь, за определённый промежуток времени зависит от его скорости;

Здесь путь обозначается буквой S и измеряется в метрах, скорость обозначается буквой вэ и измеряется в метрах в секунду, время движения обозначается буквой t и измеряется в секундах.

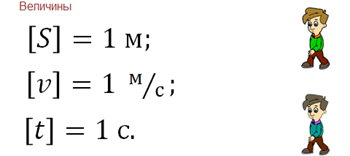
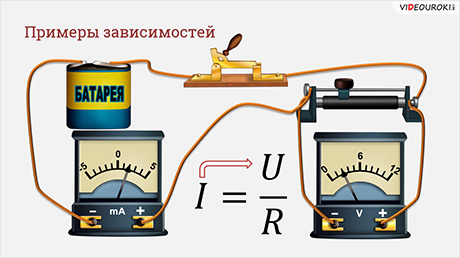
В следующем примере мы рассматривали зависимость силы тока, которая обозначается буквой I и измеряется в Амперах, от напряжения, обозначается буквой U и измеряется в Вольтах. Сопротивление обозначается буквой R и измеряется в Омах.

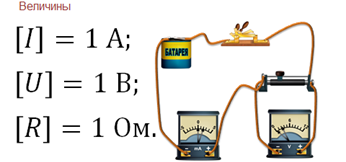
Далее, загрязнённость воздуха будем характеризовать концентрацией различных примесей. Обозначим буквой C, измеряется в миллиграммах на метр кубический. Здесь единица измерения — это масса примесей, содержащихся в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости характеризовать числом хронических больных астмой, приходящихся на тысячу жителей данного города. Обозначим буквой P, измеряется в больной на тысячу.

Также важно отметить различия зависимостей в приведённых примерах.

В первом и втором примерах зависимость между величинами является полностью определённой: значение пути точно зависит от скорости, а сила тока точно зависит от напряжения. В третьем примере зависимость между загрязнённостью воздуха и уровнем заболеваемости более сложная. Так как на уровень заболеваемости влияют и многие другие факторы.

То есть на математическом языке в первом и втором примере зависимости являются функциональными, а в третьем нет.

Как вы помните из прошлого урока модели могут быть материальные и информационные. 

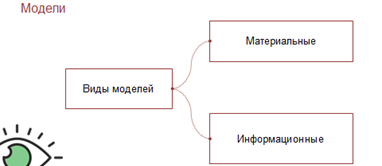
В ходе материального моделирования изготавливается макетный или опытный образец технического объекта, и проводятся его испытания по определению выходных параметров, характеристик и степени надёжности. Основной недостаток такого метода – большие временные и материальные затрат.

К информационному относится математическое моделирование. Если зависимость между величинами удаётся представить в математической форме, то мы имеем математическую модель.

Математической моделью называется совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности изучаемого объекта, процесса или явления.

Запишем математические модели для наших зависимостей.

В первом случае путь равен скорость умножить на время. Такая зависимость называется линейной.

Во втором случае сила тока равна напряжение разделить на сопротивление. Здесь сила тока прямо пропорционально зависит от напряжения и зависимость называется линейной. Также сила тока обратно пропорционально зависит от сопротивления и зависимость называется обратной пропорциональностью.

Более сложные математические модели представляются в виде уравнений, неравенств или их систем.

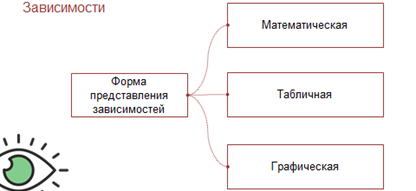
Мы выяснили что, зависимости между величинами можно представлять в математической форме. Ещё зависимости можно представлять в табличной и графической форме.

Предположим мы решили проверить зависимость пути от времени при равномерном движении. Пусть скорость пешехода равна одна целая пять десятых метров в секунду. Будем увеличивать каждый раз длину пути на три метра, и измерять время, за которое пешеход будет проходить данный путь.

Результаты измерений занесём в таблицу и нарисуем график.

Если мы возьмём из таблицы пару значений c и t и подставим в формулу пути, то формула превратится в равенство. Значит, можно сделать вывод, что модель работает правильно. 

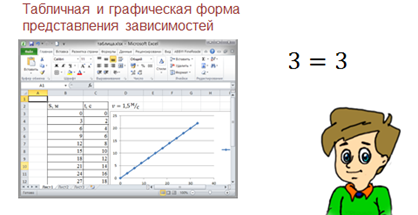
В этом примере мы рассмотрели три способа моделирования зависимости величин: функциональный (формула), табличный и графический.

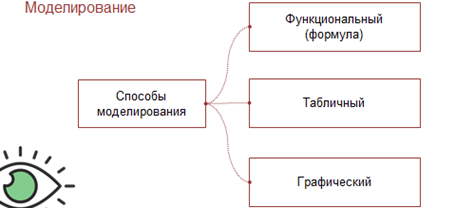
Однако математической моделью равномерного движения тела можно назвать только формулу. Формула более универсальна, она позволяет определить время движения тела на любом участке пути, а не только для экспериментального набора значений пути.

Имея формулу, можно легко создать таблицу и построить график, а вот наоборот по таблице или графику вывести формулу — весьма проблематично.

Точно так же тремя способами можно отобразить зависимость силы тока от напряжения. Оба примера связаны с известными физическими законами. Знания физических законов позволяют производить точные расчёты, они лежат в основе современной техники.

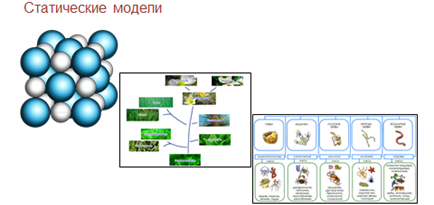
Информационные модели, описывающие объекты, явления, процессы в определённый момент времени, без учёта их изменений в пространстве и времени, называются статическими.

Такими моделями являются, например, структура кристаллов, классификация растений или животных.

Динамические модели учитывают изменения параметров процессов и явлений с течением времени.

В первом примере приведена именно такая модель.

В физике динамические информационные модели описывают движение тел, в биологии — развитие организмов или популяций животных, в химии — протекание химических реакций и т. д.

Завершая наш урок, давайте повторим всё, что мы сегодня изучили:

Количественной характеристикой исследуемого объекта является величина. Понятие величина включает три свойства: имя, значение, тип.

Математической моделью называется совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности изучаемого объекта, процесса или явления.

Отображать зависимости между величинами можно: математически с помощью формулы, таблично и графически.

Динамические модели учитывают изменения параметров процессов и явлений с течением времени.