Клеточки на бумаге позволяют многие построения проводить только с помощью линейки, причём на этой линейке может даже не быть делений. Но всегда нужно помнить свойства геометрических фигур, ведь именно они позволяют использовать клеточки в полной мере.
Давайте разделим отрезок 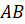 пополам. Для этого начертим прямоугольник так, чтобы данный
отрезок был его диагональю. Мы знаем, что диагонали прямоугольника при
пересечении делятся пополам. Тогда проведём в нашем прямоугольнике вторую
диагональ и таким образом разделим отрезок
пополам. Для этого начертим прямоугольник так, чтобы данный
отрезок был его диагональю. Мы знаем, что диагонали прямоугольника при
пересечении делятся пополам. Тогда проведём в нашем прямоугольнике вторую
диагональ и таким образом разделим отрезок 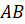 на два равных отрезка.
на два равных отрезка.
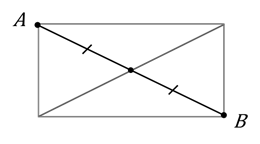
Много интересного можно получить из экспериментов с прямоугольным треугольником на клетчатой бумаге.
Изобразим произвольный прямоугольный треугольник. А затем повернём
его на 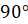 , например, против часовой стрелки.
, например, против часовой стрелки.
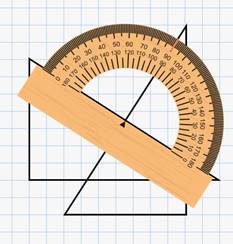
Измерим угол между большими сторонами (гипотенузами) получившихся
треугольников. Для этого воспользуемся транспортиром. Приложим его таким
образом, чтобы точка пересечения сторон совместилась с серединой основания
транспортира, а одна из сторон прошла через начало отсчёта на шкале
транспортира. Теперь находим штрих на шкале, через который проходит другая
сторона. Помним, что мы используем ту шкалу, на которой располагается 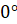 .
.
Видим, что этому штриху соответствует 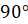 , а значит, угол между большими сторонами треугольников прямой.
, а значит, угол между большими сторонами треугольников прямой.
Таким образом, поворачивая треугольник на 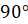 , мы тем самым поворачиваем все его элементы, в том числе и
стороны, на тот же угол, значит, угол между большими сторонами также равен
, мы тем самым поворачиваем все его элементы, в том числе и
стороны, на тот же угол, значит, угол между большими сторонами также равен 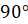 .
.
Используя результат этого опыта, выполним задание. Постройте перпендикуляр к отрезку, соединившему два любых узла клетчатой бумаги.
Решение. Проведём отрезок, который
соединяет два произвольных узла бумаги в клетку. Затем достроим отрезок до
прямоугольного треугольника так, чтобы данный отрезок являлся гипотенузой, то
есть большей стороной, а затем повернём треугольник на 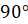 вокруг произвольной точки.
вокруг произвольной точки.
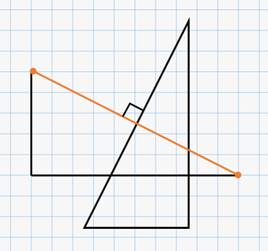
Получается, что гипотенуза получившегося треугольника является перпендикуляром к заданному отрезку.
Иногда бывают случаи, когда надо нарисовать окружность, а циркуля нет, но есть бумага в клетку.
На одном из предыдущих занятий мы с вами познакомились с правилом
(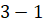 ,
, 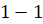 ,
, 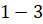 ), которое позволяет изобразить окружность на клетчатой бумаге от
руки. Правда, речь шла об окружности, радиус которой равен 5 клеткам.
), которое позволяет изобразить окружность на клетчатой бумаге от
руки. Правда, речь шла об окружности, радиус которой равен 5 клеткам.
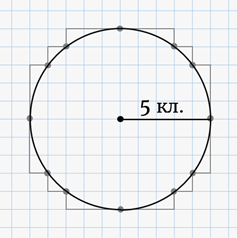
Сейчас мы выведем правило, с помощью которого от руки можно изобразить окружность, радиус которой равен 13 клеткам.
Для удобства с помощью циркуля начертим окружность с радиусом 13 клеток с центром в узле клеток.
Итак, возьмём узел клетчатой бумаги на данной окружности. Отступив на 1 клетку вправо и на 5 клеток вверх, поставим вторую точку. Отступая от второй точки вправо на 1 клетку и вверх на 2 клетки, ставим третью точку. Далее, отступив 4 клетки вправо и 4 клетки вверх, находим четвёртую точку. Отступив 2 клетки вправо и 1 клетку вверх, поставим 5 точку. Шестая точка находится на расстоянии 5 клеток вправо и 1 клетки вверх от пятой точки.
Если соединить эти шесть точек плавной линией, получим четверть окружности.
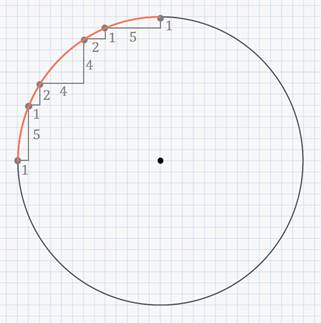
Чтобы достроить окружность нам надо повторить эти действия ещё три раза, изменяя направление движения.
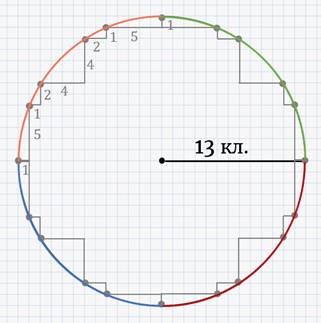
Правило, с помощью которого можно построить окружность с радиусом,
равным 13и клеткам, можно записать следующим образом: 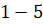 ,
, 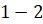 ,
, 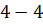 ,
, 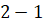 ,
, 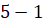 .
.
Вернёмся к выполнению заданий. Найдите площадь
прямоугольного треугольника (с катетами 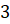 клетки и
клетки и 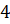 клетки), если все его вершины лежат в узлах клеток, а две стороны
проходят по сторонам клеток. Площадь одной клетки примем за единицу.
клетки), если все его вершины лежат в узлах клеток, а две стороны
проходят по сторонам клеток. Площадь одной клетки примем за единицу.
Решение. Изобразим прямоугольный треугольник так, чтобы все его вершины лежали в узлах клеток, а две стороны проходили по сторонам клеток.
Затем достроим этот треугольник до прямоугольника так, чтобы вершины нашего треугольника совпали с вершинами прямоугольника, а стороны, которые являются катетами нашего треугольника, лежали на сторонах прямоугольника. Затем сосчитаем количество клеточек в прямоугольнике. Их 12. То есть площадь прямоугольника равна 12 (ед. кв.).
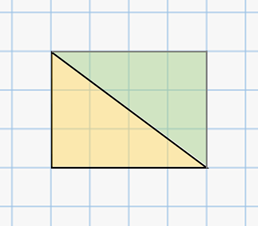
Заметим, что построенный прямоугольник состоит из двух равных прямоугольных
треугольников. Тогда площадь нашего треугольника равна половине площади
прямоугольника. А это 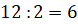 (ед. кв.).
(ед. кв.).
Следующее задание. Начертите два разных прямоугольных треугольника, площади которых равны 2 клеткам.
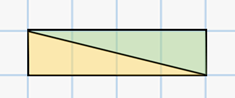
Решение. Давайте изобразим два прямоугольника, площади которых равны 4 клеткам.
Это прямоугольник со сторонами, равными 1 клетке и 4 клеткам. И квадрат со стороной, равной 2 клеткам.
Теперь в прямоугольнике проведём диагональ, которая разделит его
на два равных прямоугольных треугольника. Площадь каждого из них будет равна 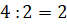 (кл.).
(кл.).
Проведём диагональ в квадрате. Она разделит его на два равных
прямоугольных треугольника. Площадь каждого из них будет равна 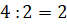 (кл.).
(кл.).
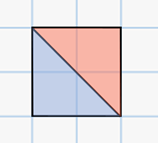
Так, мы получили два различных прямоугольных треугольника, площадь каждого из которых равна двум клеткам.
Эта задача показывает, что для равенства фигур ещё недостаточно равенства их площадей.
Сейчас мы с вами познакомимся с формулой Пика, которая названа именем математика Георга Пика. В 16 лет он окончил школу и поступил в Венский университет. В возрасте 17 лет была опубликована его первая работа. Круг его математических интересов был очень широк. 67 его работ посвящены многим разделам математики.
Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника.
C помощью формулы Пика можно вычислить площадь произвольного многоугольника с вершинами в узлах клетки. Формула имеет вид:

Здесь 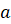 – число узлов внутри многоугольника,
– число узлов внутри многоугольника, 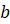 – число узлов на границе многоугольника, включая вершины.
– число узлов на границе многоугольника, включая вершины.
Найдём площадь изображённого многоугольника. Для этого сосчитаем число узлов внутри многоугольника. Оно равно 10. Теперь сосчитаем число узлов на границе, включая вершины. Оно равно 7.
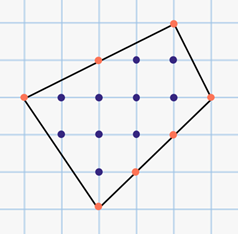
Подставим полученные значения в формулу: 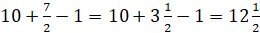 (ед. кв.).
(ед. кв.).
Получили, что площадь данного многоугольника равна 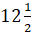 (ед. кв.).
(ед. кв.).
Выполним задание. Найдите площадь многоугольника, изображённого на рисунке.
Решение.



 Получите свидетельство
Получите свидетельство Вход
Вход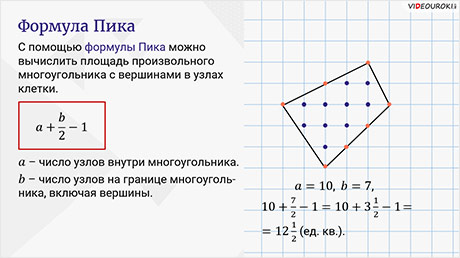




 7773
7773



