Умножение многочлена на многочлен

Вопросы занятия:

·  повторить правило умножения одночлена на многочлен;

·  показать правило умножения многочлена на многочлен.

Материал урока

На одном из предыдущих уроков мы говорили об умножении одночлен на многочлен.

На этом уроке мы научимся умножать многочлен на многочлен.

Итак, возьмём два многочлена:

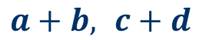
Составим их произведение

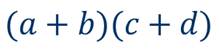
Обозначим:

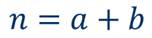
тогда выражение примет вид

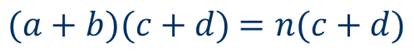
Теперь воспользуемся правилом умножения одночлена на многочлен, которое мы повторили в начале урока, и получим

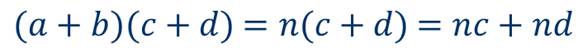
Далее вернёмся к замене,

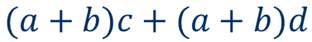
Снова воспользуемся правилом умножения одночлена на многочлен и получим

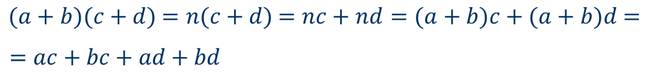
Таким образом, мы представили произведение многочленов в виде суммы.

Обратите внимание, что полученный в результате многочлен представляет собой сумму одночленов, которые получаются при умножении каждого слагаемого многочлена (a + b) на каждое слагаемое многочлена (c + d).

Следовательно, для того, чтобы умножить многочлен на многочлен, надо:

1.  каждый член одного многочлена умножить на каждый член другого многочлена;

2.  полученные произведения сложить.

Произведение многочлена на многочлен является многочленом.

При этом обратите внимание, что при умножении многочлена на многочлен до приведения подобных слагаемых у нас всегда должно получаться количество слагаемых, равное произведению числа слагаемых первого и второго многочленов.

Пример.

Пример.

Пример.