Сегодня на уроке мы вспомним, какие события называются элементарными. Узнаем, что называется суммой событий. Выясним, что называется произведением событий. Скажем, какие события называются равносильными. Поговорим о противоположных событиях.
Предположим, что в результате некоторого испытания обязательно происходит одно из взаимно исключающих друг друга событий, причём каждое из них не разделяется на более простые (элементарные). Такие события называют элементарными событиями (или элементарными исходами испытания).
Пусть в некотором испытании могут произойти события  и
и  . Давайте рассмотрим комбинации этих событий.
. Давайте рассмотрим комбинации этих событий.
Итак, суммой (объединением) событий  и
и  называется событие, которое состоит в том, что происходит хотя бы
одно из данных событий. Сумму событий
называется событие, которое состоит в том, что происходит хотя бы
одно из данных событий. Сумму событий  и
и  обозначают
обозначают  (или
(или  ).
).
Сейчас вы видите рисунок, на котором проиллюстрировано понятие
суммы событий  и
и  с помощью кругов Эйлера.
с помощью кругов Эйлера.

Большой круг изображает все элементарные события, которые могут
произойти в рассматриваемом испытании, левый круг изображает событие  , правый круг – событие
, правый круг – событие  , а закрашенная область – объединение событий
, а закрашенная область – объединение событий  и
и  .
.
Произведением (пересечением)
событий  и
и  называется событие, которое состоит в том,
что происходят оба этих события. Произведение событий
называется событие, которое состоит в том,
что происходят оба этих события. Произведение событий  и
и  обозначают
обозначают  (или
(или  ).
).
Следующий рисунок иллюстрирует с помощью кругов Эйлера
произведение событий  и
и  .
.

Общая часть кругов (закрашенная область) изображает пересечение
событий  и
и  .
.
Приведём примеры.
Предположим, что испытание состоит в определении числа на верхней
грани игрального кубика после одного броска, при этом событие  – выпало число очков, кратное двум, событие
– выпало число очков, кратное двум, событие  – выпало число очков, кратное трём. Тогда событие
– выпало число очков, кратное трём. Тогда событие  означает, что на верхней грани кубика появится хотя бы одно из
чисел 2, 3, 4, 6.
означает, что на верхней грани кубика появится хотя бы одно из
чисел 2, 3, 4, 6.
Событие  означает выпадение чётного числа, кратного
трём. Такое число одно – это 6.
означает выпадение чётного числа, кратного
трём. Такое число одно – это 6.
Допустим, что испытание заключается в том, что из колоды
вынимается наудачу одна карта, и пусть рассматриваются следующие события:
событие  – вынут король, событие
– вынут король, событие  – вынута карта пиковой масти. Тогда событие
– вынута карта пиковой масти. Тогда событие  – вынут король или карта пиковой масти. Событие
– вынут король или карта пиковой масти. Событие  – из колоды карт вынут король пик.
– из колоды карт вынут король пик.
Теперь поговорим о равносильных событиях. Итак, события  и
и  называют равносильными (равными) и пишут
называют равносильными (равными) и пишут  , если событие
, если событие  происходит тогда и только тогда, когда происходит событие
происходит тогда и только тогда, когда происходит событие  .
.
Так, например, в испытании с одним бросанием игрального кубика
событие  – выпала единица и событие
– выпала единица и событие  – выпало наименьшее число очков являются равносильными. Можно
записать, что
– выпало наименьшее число очков являются равносильными. Можно
записать, что  .
.
Для каждого события  можно рассматривать противоположное для него событие
можно рассматривать противоположное для него событие  , которое считается наступившим тогда и только тогда, когда
событие
, которое считается наступившим тогда и только тогда, когда
событие  не наступает.
не наступает.
Например, если событие  – выпадение нечётного числа очков при бросании игрального кубика,
то событие
– выпадение нечётного числа очков при бросании игрального кубика,
то событие  , – выпадение чётного числа очков. Если событие А – попадание в
цель при выстреле, то событие
, – выпадение чётного числа очков. Если событие А – попадание в
цель при выстреле, то событие  , – промах. Если событие А – появление орла при одном
подбрасывании монеты, то событие
, – промах. Если событие А – появление орла при одном
подбрасывании монеты, то событие  – появление решки.
– появление решки.
На следующем рисунке проиллюстрирована взаимосвязь события А
и противоположного события  на множестве всех элементарных исходов испытания.
на множестве всех элементарных исходов испытания.

Здесь событие  изображено закрашенной областью.
изображено закрашенной областью.
Далее рассмотрим задачу. Пусть  и
и  – два произвольных события. Запишем с помощью введённых
обозначений события:
– два произвольных события. Запишем с помощью введённых
обозначений события:
1)  – оба события произошли;
– оба события произошли;
2)  – произошло только событие
– произошло только событие  ;
;
3)  – ни одно из событий
– ни одно из событий  и
и  не произошло;
не произошло;
4)  – произошло по крайней мере одно из событий
– произошло по крайней мере одно из событий  и
и  ;
;
5)  – произошло либо только событие
– произошло либо только событие  , либо только событие
, либо только событие  .
.
Решение.

Теперь пусть  ,
,  ,
,  – три произвольных события. Запишем с помощью введённых
обозначений события:
– три произвольных события. Запишем с помощью введённых
обозначений события:
1)  – все три события произошли;
– все три события произошли;
2)  – ни одно событие не произошло;
– ни одно событие не произошло;
3)  – произошло только событие
– произошло только событие  ;
;
4)  – произошло по крайней мере одно из событий
– произошло по крайней мере одно из событий  ,
,  ,
,  .
.
Решение.

А сейчас давайте выполним несколько заданий.
Задание первое. Пятнадцать карточек
пронумерованы числами от  до
до  . Произвольно из них выбирается одна карточка. Пусть событие
. Произвольно из них выбирается одна карточка. Пусть событие  – на карточке записано число, кратное
– на карточке записано число, кратное  ; событие
; событие  – на карточке записано число, кратное
– на карточке записано число, кратное  . Выясните, в чём состоят события
. Выясните, в чём состоят события  и
и  .
.
Решение.

Задание второе. Установить, что является событием, противоположным каждому из событий:
1) сегодня первый урок – физика;
2) экзамен сдан на отлично;
3) при одном броске монеты выпал орёл;
4) хотя бы одна пуля при трёх выстрелах попала в цель;
5) из колоды карт извлечена шестёрка;
6) на игральной кости выпало меньше четырёх очков;
7) хотя бы на одной из двух брошенных игральных костей появилось
число  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход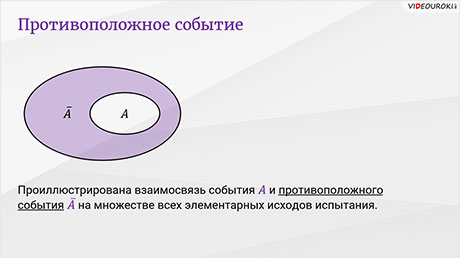




 5475
5475