Производная

Вспомним основные моменты. Пусть 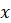 – произвольная точка, которая лежит в некоторой окрестности фиксированной точки 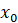. Разность  называется приращением независимой переменной (или приращением аргумента) в точке 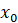 и обозначается .

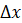Таким образом, 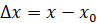. Тогда .

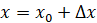Говорят, что первоначальное значение аргумента 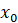 получило приращение .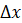

При этом, если мы изменяем аргумент, то и значение функции 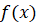 тоже будет изменяться на величину:

.

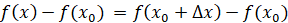Приращением функции 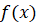 в точке 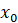, соответствующим приращению 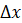, называется разность 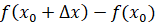 и обозначается дельта .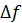

Напомним, что производной функции 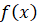 в точке  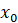называется предел отношения приращения функции в этой точке  к приращению аргумента 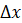 при .

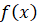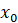Если функция  имеет производную в точке , то данная функция называется дифференцируемой в этой точке.

Если функция 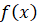 имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке.

Операция нахождения производной называется дифференцированием.

Геометрический смысл производной заключается в том, что значение производной функции 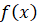 в точке  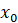равно угловому коэффициенту касательной к графику функции в точке с координатами , то есть , где  – угол между касательной и осью .

Уравнение касательной к графику функции 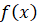, дифференцируемой в точке 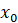, имеет вид:

.

Физический смысл производной. Если точка движется вдоль оси  и её координата изменяется по закону , то мгновенная скорость точки , а ускорение .

Напомним правила нахождения производной. Если функции  и  имеют производные, то:

;

;

;

, .

Также вспомним, как находить производную сложной функции. Если функция  имеет производную в точке 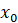, а функция  имеет производную в точке , то сложная функция  также имеет производную в точке 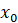, причём

.

На следующем слайде приведены производные основных элементарных функций.

Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.

Задание первое. Составьте уравнение касательной к графику функции  в точке с абсциссой .

Решение.

Задание второе. Чему равен угловой коэффициент касательной к графику  в точке с абсциссой ?

Решение.

Задание третье. Точка движется вдоль оси , и её координата изменяется по закону . Найдите скорость точки в момент времени .

Решение.

Задание четвёртое. Найдите производные функций:

а) ;

б) ;

в) ;

г) .

Решение.

Задание пятое. Найдите производные функций:

а) ;

б) ;

в) ;

г) .

Решение.