Основные формулы и методические рекомендации по решению задач на механические колебания

«Все, что казалось трудным нам сначала,

к концу обычно трудным не бывало».

В данной теме рассмотрим основные формулы и методические рекомендации по решению задач на механические колебания.

Выделяют три основных вида колебаний: свободные колебания, вынужденные колебания, и автоколебания. Свободные колебания происходят только под действием возвращающей силы, то есть за счёт первоначальной энергии сообщённой системе. Вынужденные колебания происходят под действием некой внешней силы, которая периодически изменяется. Эту силу иногда называют вынуждающей силой. Наконец, автоколебания происходят при периодическом поступлении энергии от источника, находящегося внутри колебательной системы. В данном разделе будем преимущественно рассматривать свободные колебания, а также уделим время вынужденным колебаниям.

Гармонические колебания – это повторяющийся во времени процесс отклонения системы от положения равновесия, при котором не происходят потери энергии, и который подчиняется синусоидальному закону. Соответственно, в случае механических колебаний, зависимость координаты от времени будет представлять собой синусоиду.

Математический маятник – это осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения.

Пружинный маятник представляет собой механическую систему, состоящую из пружины, подчиняющейся закону Гука, один конец которой жёстко закреплён, а на втором находится груз.

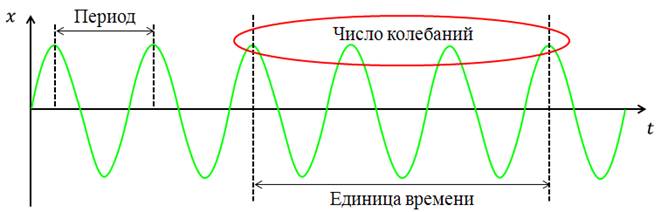
Рассмотрим характеристики колебательного движения. Амплитудой колебаний называется максимальное отклонение колеблющейся величины от положения равновесия. Для примера рассмотрим график, описывающий гармонические колебания. Положения максимального отклонения соответствуют пикам синусоиды. Фаза – это величина, определяющая смещение в любой момент времени (то есть, состояние системы). Если обозначить на графике вторую синусоиду, то фазой будет расстояние между двумя ближайшими пиками этих синусоид.

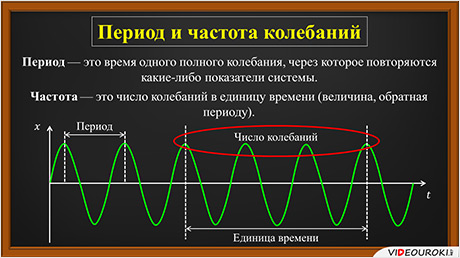
Периодом колебаний называется время одного полного колебания (то есть, за это время повторяются какие-либо показатели системы). Для примера рассмотрим график, описывающий гармонические колебания. Расстояние между двумя ближайшими пиками синусоиды – это и будет промежуток времени, по прошествии которого повторились показатели системы (в данном случае, это отклонение от положения равновесия). Частота колебаний – это величина, обратная периоду, то есть, число колебаний в единицу времени.

Циклическая частота – это физическая величина, численно равна количеству колебаний за 2p секунд. Собственная частота – это частота колебаний системы при отсутствии сил сопротивления в среде.

Сведём в таблицу основные формулы механических колебаний.

Обобщённо задачи, которые будут рассматриваться в данном разделе, можно разделить на две группы: задачи на применение общих уравнений гармонических колебаний и задачи о математических или пружинных маятниках.

Методические рекомендации по решению задач на применение общих уравнений гармонических колебаний

1. Записать общее уравнение гармонических колебаний.

2. Если в задаче есть заданное уравнение колебаний, сопоставить его с общим уравнением и определить характеристики колебательного движения.

3. Если в задаче даны характеристики колебательного движения, составить уравнение колебательного движения, опираясь на них.

Методические рекомендации по решению задач на математические и пружинные мятники

1. Построить рисунок, обозначив на нём необходимые величины.

2. Установить начальное и конечное положения системы.

3. Выбрать нулевой уровень потенциальной энергии.

4. Определить какие превращения энергии происходят в системе.

5. На основании этого составить систему уравнений и решить её относительно искомых величин.