Представим себе такую историю…
– Саша, чем ты занимаешься? – поинтересовался у друга Паша.
– Нам по математике задали разгадать ребус, по которому мы узнаем тему нашего следующего урока, – ответил Саша. — Но я забыл, как разгадываются ребусы.
– Не расстраивайся! – подбодрил друга Паша. – Я помогу тебе. Показывай свой ребус.
– Вот, смотри, какое загадочное слово! – воскликнул Саша.
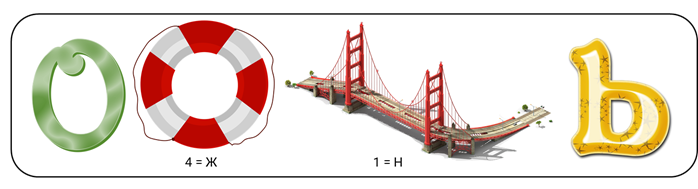
– Саша, да это совсем лёгкий ребус, – отметил Паша. – Сейчас мы быстренько всё разгадаем. Итак, твой ребус начинается с буквы «О». Букву эту и оставим на первом месте. Затем нарисована картинка, а под ней равенство цифры и буквы. Напомню, что знак равенства, изображённый возле картинки, служит для обозначения замены одной из букв на другую. У тебя нарисован круг, а снизу равенство, указывающее, что нужно четвёртую букву в названии картинки заменить на букву «Ж». Что за слово получится после замены?
– Был «круг», заменим четвёртую букву на «Ж», значит, у нас получится «круж», – сказал Саша.
– Отлично! – поддержал друга Паша. – Идём дальше. Здесь нарисован мост и снова под картинкой равенство цифры и буквы. Что за слово получится?
– В слове «мост» нужно заменить букву «м» на букву «н», – начал размышлять Саша. – Тогда после замены получим слово «ност».
– Верно! – согласился Паша. – И заканчивается твой ребус буквой «ь». Эта буква и будет завершать всё слово. А теперь попробуй из получившихся слов и букв составить единое слово.
– Так, – начал Саша, – у нас есть буква «О», слово «круж», слово «ност» и буква «ь». Подумаем… Так это же «окружность»!
– Молодец, Саша! – похвалил друга Паша. — Значит, на уроке математики вы будете знакомиться с окружностью!

– Интересно, а что же нам про неё расскажут? – спросил Саша.
– А давай обратимся к Мудряшу, – предложил Паша. – Он точно сможет много интересного рассказать об этой замечательной геометрической фигуре.
– Ребята, прежде чем я расскажу вам об окружности и круге, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Многие предметы нашего окружения имеют формы, похожие на определённые геометрические фигуры. Давайте посмотрим на следующие предметы из нашей жизни. Скажите, что их всех объединяет?
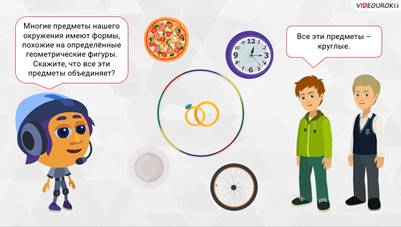
– Все эти предметы — круглые, – заметил Саша.
– Правильно! – согласился Мудряш. – А что вы можете сказать об их форме? На какие геометрические формы они похожи?
– Кольца, гимнастический обруч и колесо велосипеда имеют форму окружности, – сказал Паша, – а вот пицца, тарелка и настенные часы – форму круга.
– Всё верно! – обрадовался Мудряш. – В начальных классах вы уже знакомились с этими фигурами. Чтобы разобраться, что такое окружность и чем она отличается от круга, необходимо иметь чёткое представление об этих фигурах. И начнём мы, пожалуй, разговор с окружности. Итак, вы уже знаете, что окружность легко начертить с помощью циркуля. Давайте вспомним, как происходит этот процесс.
– Для того чтобы начертить окружность, мы должны установить остриё циркуля (иглу) на бумагу, – начали рассказывать мальчишки. – А вторую ножку циркуля, которая с карандашом, нужно вращать вокруг первой. Карандаш начертит на плоскости листа линию, которая и называется окружностью.

– Молодцы! – похвалил ребят Мудряш. – Запомните! Окружность – это геометрическая фигура на плоскости, все точки которой равноудалены от данной точки – центра окружности. Точка, в которой устанавливалось остриё циркуля (игла), называется центром окружности. Как правило, центр окружности обозначают точкой О.
– О чём говорит фраза «все точки которой равноудалены от данной точки»? – спросил у ребят Мудряш.
– Это значит, что все точки окружности удалены от её центра на одинаковое расстояние, – ответили мальчишки.
– Правильно! – согласился Мудряш. – Кстати, именно этот факт позволяет любому транспортному средству на колёсах ехать ровненько, так как при движении транспортного средства центр колеса всегда находится на одинаковом расстоянии от земли.

– А теперь давайте соединим центр окружности, то есть нашу точку О, с любой понравившейся вам точкой на окружности, – продолжил Мудряш. – Обозначим эту точку, например буквой А. Видим, что у нас получился отрезок ОА.

Запомните! Отрезок, соединяющий центр окружности с любой её точкой, лежащей на окружности, называют радиусом.
– А если мы ещё поставим точки на окружности, например В и К, и соединим эти точки с центром окружности, – решили спросить мальчишки, – отрезки ОВ и ОК тоже будут радиусами?
– Верно! – ответил Мудряш. – На нашем рисунке отрезки ОА, ОВ, ОК – радиусы окружности. Причём все радиусы одной окружности равны между собой. То есть радиусы ОА, ОВ и ОК равны.

– Давайте измерим длину нашего радиуса О А, – сказал Мудряш.
– Эта длина равна 2,5 сантиметра, – померили мальчишки.
– Хорошо! – продолжил Мудряш. – Говорят, что длина радиуса ОА равна 2,5 сантиметра. Но зачастую слово «длина» не произносят, а вместо «длина радиуса» говорят просто «радиус». То есть можно сказать, что радиус окружности равен 2,5 сантиметра. Радиус окружности принято обозначать буквой r. Тогда для нашей окружности можно записать, что r = 2,5 сантиметра.

– А теперь давайте отметим любые две точки на окружности, например M и N, и соединим их отрезком. Видим, что у нас получился отрезок MN.

Запомните! Отрезок, соединяющий любые две точки окружности, называют хордой.
– А если бы мы отметили точки Е и F вот так:… и соединили бы их отрезком, то отрезок ЕF тоже являлся бы хордой? – решили уточнить мальчишки.
– Отрезок ЕF — тоже хорда, – ответил Мудряш. – Только у этой хорды есть собственное название.
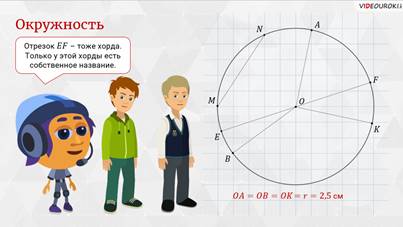
Запомните! Отрезок, соединяющий две точки на окружности и проходящий через центр окружности, называют диаметром окружности.
– Если посмотреть внимательно на диаметр ЕF, – заметил Паша, – то увидим, что диаметр состоит из 2 радиусов.
– Ты очень внимательный! – сказал Мудряш. – Диаметр окружности равен двум её радиусам. Поэтому диаметр в 2 раза больше радиуса. Диаметр окружности принято обозначать буквой d. Значит, можем записать, что d = 2r.
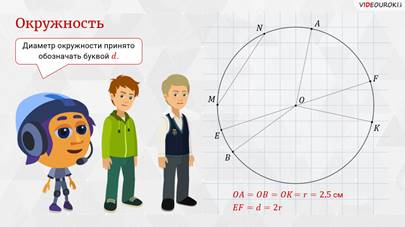
– Две точки, лежащие на окружности, например Е и F, делят её на 2 части, – продолжил Мудряш. – Каждую из этих частей называют дугой окружности. Точки Е и F называют концами дуг.

– Ну, с окружностью всё понятно, – сказал Саша, – а чем же тогда отличается круг от окружности? Он тоже круглый.
– Любая окружность разделяет плоскость на две части, – начал Мудряш. – Ту часть плоскости, которая лежит внутри окружности вместе с самой окружностью, называют кругом.
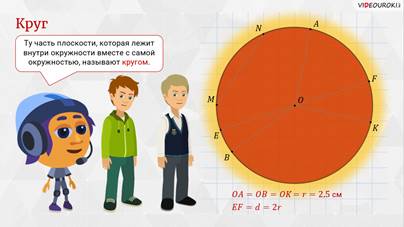
Круг имеет центр, радиус, диаметр, хорду – это соответственно центр, радиус, диаметр, хорда окружности, ограничивающей круг. Назовите элементы нашего круга.
– Точка О – это центр круга, – сказал Саша. – Отрезки ОА, ОB и ОК – его радиусы.
– Отрезок MN – это хорда нашего круга, – ответил Паша, – а вот отрезок ЕF – это его диаметр.
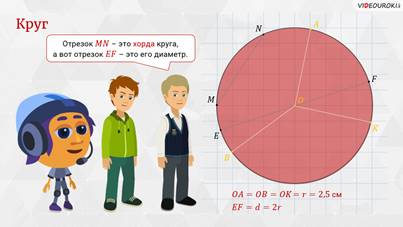
– Молодцы! – похвалил ребят Мудряш. – Если из центра О круга провести два радиуса, например ОА и ОB, то они разделят круг на две части. Каждую из этих частей называют сектором.
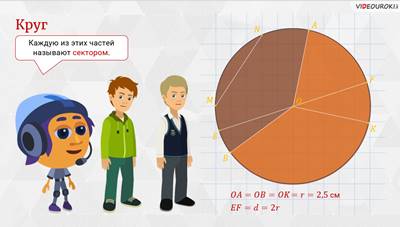
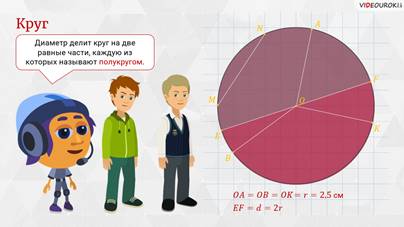
А что касается нашего диаметра ЕF, то он делит круг на две равные части, каждую из которых называют полукругом.
– Несложно догадаться, что точки могут лежать на окружности (мы будем говорить «принадлежат окружности»), а могут и не лежать на ней, то есть не принадлежать окружности. Аналогично и с кругом, – продолжил Мудряш. – Например, точки А, B и К принадлежат окружности с центром в точке О. А точки О, C и D не принадлежат окружности с центром в точке О. В свою очередь, точки О, А, B, К и C принадлежат кругу с центром в точке О. А вот точка D не принадлежит этому кругу. При этом точка D удалена от центра круга на расстояние, большее радиуса.

Запомните! Если точка удалена от центра круга на расстояние, меньшее радиуса круга или равное ему, то эта точка принадлежит кругу.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: начертите окружность радиусом 2 сантиметра с центром в точке О. Вычислите диаметр этой окружности.
Решение: при помощи линейки сделаем раствор циркуля равным 2 сантиметрам. Ножку с иголкой поместим в точку О, а ножкой с карандашом опишем окружность. А теперь вычислим диаметр нашей окружности. Так как диаметр в 2 раза больше радиуса, то диаметр нашей окружности равен 4 сантиметрам.

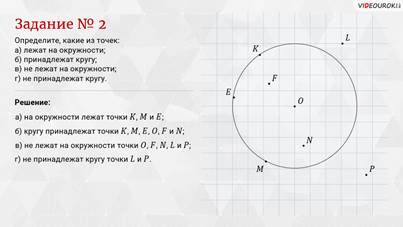
Задание второе: определите, какие из точек лежат на окружности, принадлежат кругу, не лежат на окружности, не принадлежат кругу.
Решение: на окружности лежат точки К, M и Е. Кругу принадлежат точки К, M, Е, О, F и N. Не лежат на окружности точки О, F, N, L и P. Не принадлежат кругу точки L и P.
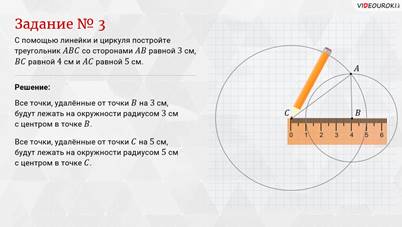
И последнее задание: с помощью линейки и циркуля постройте треугольник АBC со сторонами АB равной 3 сантиметрам, BC равной 4 сантиметрам и АC равной 5 сантиметрам.
Решение: с помощью линейки построим отрезок CB длиной 4 сантиметра. Третья вершина А треугольника должна быть удалена от точки B на 3 сантиметра, а от точки C – на 5 сантиметров. Все точки, удалённые от точки B на 3 сантиметра, будут лежать на окружности радиусом 3 сантиметра с центром в точке B. Построим эту окружность. Все точки, удалённые от точки C на 5 сантиметров, будут лежать на окружности радиусом 5 сантиметров с центром в точке C. Построим вторую окружность. Следовательно, точка А будет точкой пересечения этих окружностей. Соединим точку А с точками B и C. Мы получили искомый треугольник АBC.

 Получите свидетельство
Получите свидетельство Вход
Вход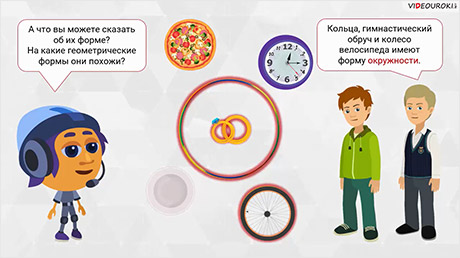



 0
0 4510
4510

