Измерение частоты и периода колебаний математического маятника

Цель первой части нашей работы: с помощью экспериментальной установки определить период свободных колебаний математического маятника заданной длины.

Оборудование мы будем использовать из пятого комплекта, а именно: штатив с муфтой и креплением для нити, груз с крючком, нить, электронный секундомер, метровую линейку или мерную ленту, возможно вам понадобится и транспортир.

Своеобразные движения, которые называются колебательными или просто колебаниями, всем вам хорошо известны. Они широко распространены в окружающем нас мире. Однако при всём разнообразии колебательных движений у всех них есть одна важная особенность: через определённый промежуток времени движение любого из этих тел повторяется.

Давайте вспомним, что процесс, при котором какая-либо физическая величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около своего положения равновесия называется механическим колебанием. И если силы сопротивления будут отсутствовать, то такое движение будет повторяться бесконечно долго, то есть колебания будут являться свободными.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел. Так вот, совокупность тел, в которой могут происходить колебательные процессы, мы с вами будем называть механической колебательной системой.

Вы знаете, что для упрощённого рассмотрения тех или иных явлений в науке часто пользуются идеальными моделями. Для колебательных систем такими моделями являются маятники. В общем случае маятником называется твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

Существует несколько видов маятников. Но наиболее часто встречающиеся, это пружинный маятник, представляющий собой груз, прикреплённый к пружине, и способный совершать колебания вдоль горизонтальной или вертикальной оси.

И нитяной маятник — шарик, подвешенный на нити, способный совершать колебательное движение.

Физической моделью обычного нитяного маятника является математический маятник, с которым нам с вами и предстоит сегодня работать. (Математический маятник — это материальная точка, подвешенная на конце невесомой нерастяжимой нити.)

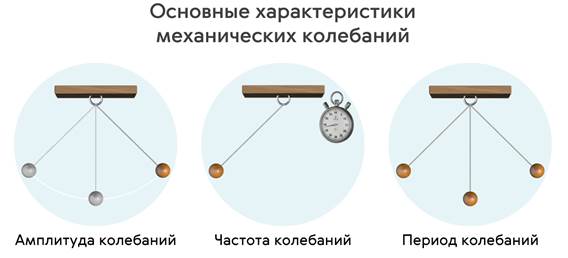
Теперь давайте вспомним, что любое колебательное движение характеризуется амплитудой, частотой и периодом колебаний.

Амплитуда колебаний — это наибольшее смещение колеблющегося тела от положения равновесия.

Частота колебаний — это число колебаний, совершаемых телом за единицу времени. Обозначается она греческой буквой «Ню» (ν). А единицей её измерения в системе СИ является герц [Гц]:

И, наконец, период колебаний — это наименьший промежуток времени, через который полностью повторяется состояние колебательной системы. Обозначается период большой буквой «Тэ» (Т). Единица измерения — секунда [с]:

Именно период колебаний мы с вами сейчас и будем искать. Итак, для начала давайте соберём экспериментальную установку. Для этого закрепим перекладину в муфте у верхнего края стержня штатива. Далее подвесим к перекладине с помощью нити один груз из набора. Расстояние от точки повеса до центра груза, то есть длина маятника, по условию задания должно быть равно 50 см. Если длины штатива не хватает и груз лежит на поверхности стола, то штатив нужно разместите на столе так, чтобы конец перекладины выступал за край поверхности стола. Электронный секундомер переведём в ручной режим работы.

Далее мы сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого много меньше длины нити — это положение равновесия маятника. Далее изображаем маятник в положении максимального отклонения (не более 15° от положения равновесия.

Теперь запишем формулы, которыми будем пользоваться при выполнении данной работы. Как мы уже вспоминали, период колебаний — это время, за которое совершается одно полное колебание. Он равен отношению промежутка времени, в течение которого тело совершило N полных колебаний, к числу этих колебаний:

С формулой всё понятно, поэтому приступим непосредственно к работе. Итак, отклоняем нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы процесс колебаний стал установившимся. В момент прохождения маятником крайнего положения запускаем секундомер. Теперь нам остаётся только дождаться, пока маятник не совершит 30 полных колебаний. По окончании последнего колебаний останавливаем секундомер.

Значение промежутка времени, за которое маятник совершил заданное число колебаний, записываем в бланк ответов с учётом погрешности измерения:

Сюда же записываем и количество колебаний, совершённых маятником:

Прямые измерения мы с вами завершили. Теперь определяем период колебаний. Для этого подставляем в расчётную формулу значения промежутка времени и числа полных колебаний:

Тогда в выводе напишем: период колебаний математического маятника равен 1,42 с.

Во второй части работы мы с вами должны с помощью экспериментальной установки определить частоту свободных колебаний математического маятника.

Оборудование мы будем использовать то же самое: штатив с муфтой и креплением для нити, груз с крючком, нить, электронный секундомер, метровую линейку или мерную ленту и транспортир.

Теория у нас остаётся та же. Только теперь мы с вами будем находить число колебаний, которые маятник совершает за единицу времени, то есть за одну секунду.

Итак, для начала давайте соберём экспериментальную установку. Для этого закрепим перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе так, чтобы конец перекладины выступал за край поверхности стола. К перекладине подвесим наш маятник, длина которого по условию задания должна быть равна одному метру (ещё раз напомним, что длину маятника мы измеряем от точки подвеса до центра груза). Электронный секундомер переведём в ручной режим работы.

Далее мы сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого много меньше длины нити — это положение равновесия маятника. Далее изображаем маятник в положении максимального отклонения (не более 15° от положения равновесия.

Теперь запишем формулы, которыми будем пользоваться при выполнении данной работы. Как мы уже вспоминали, период колебаний — это время, за которое совершается одно полное колебание:

А величина, обратная периоду, называется частотой колебаний. Таким образом, она показывает, какое количество полных колебаний совершается телом в единицу времени:

С формулами разобрались, поэтому приступим непосредственно к самой работе. Итак, отклоняем нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы процесс колебаний стал установившимся. В момент прохождения маятником крайнего положения запускаем секундомер. Теперь нам остаётся только дождаться, пока маятник не совершит 30 полных колебаний. По окончании последнего колебаний останавливаем секундомер.

Значение промежутка времени, за которое маятник совершил заданное число колебаний, записываем в бланк ответов с учётом погрешности измерения:

Здесь же указываем и количество колебаний, совершённых маятником:

Прямые измерения мы с вами завершили. Теперь определяем частоту колебаний. Для этого подставляем в расчётную формулу значения числа полных колебаний и промежутка времени, в течение которого эти колебания были совершены:

В выводе можно написать, что частота колебаний математического маятника составила примерно 0,49 Гц.