Вопросы занятия:
• рассмотреть основные этапы статистической обработки данных;
• познакомиться с понятием «дисперсия»;
• рассмотреть примеры вычисления дисперсии с помощью специального алгоритма.
Материал урока
Слово статистика происходит от латинского «статус», означающего «состояние дел».
Этому понятию можно дать следующее определение.
Статистика – отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных; изучение количественной стороны массовых общественных явлений в числовой форме.
Рассмотрим пример.
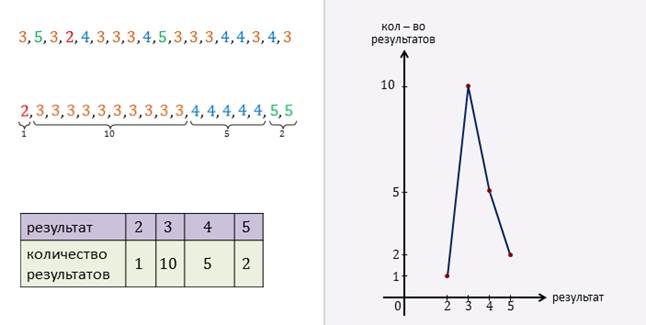
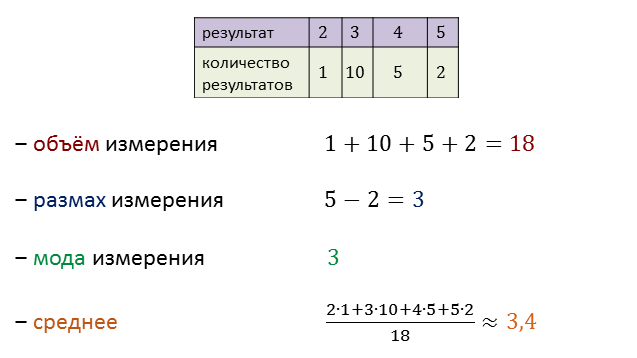
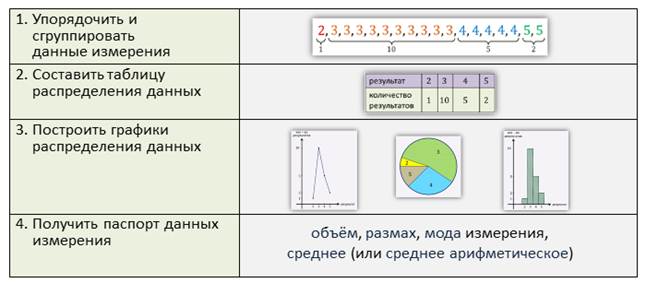
Анализируя результаты написания контрольной работы по математике, учитель сгруппировал все данные таким образом.
Только 1 человек получил двойку. Десять получили тройку. Пятеро человек написали контрольную на 4. И только двое получили пятёрки.
Всю эту информацию можно собрать в одной таблице.
Также эти данные можно представить графически.
На горизонтальной оси отметим все возможные результаты, а на вертикальной — их количество.
Так точки 2 1, 3 10, 4 5 и 5 2 будут соответствовать парам значений из таблицы. Соединим их ломаной. Так мы с вами получили многоугольник распределений.
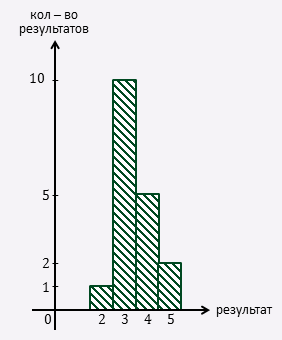
А теперь для каждой пары значений изобразим соответствующий столбец и раздуем его до ширины равной одному. Получаем столбчатую диаграмму — гистограмму распределений.
Рассмотрим ещё один способ.
Представим все данные в виде круга.
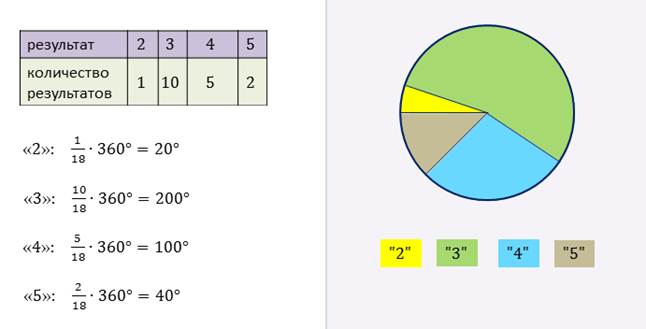
Так получается круговая диаграмма.
Сейчас мы с вами на конкретном примере разобрали основные этапы статистической обработки данных.
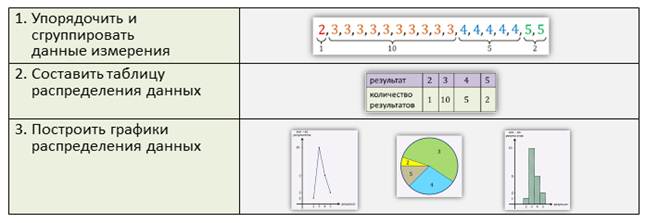
К этим трём этапам обычно добавляют ещё один: получение паспорта данных измерений, состоящий из нескольких числовых характеристик.
К этим характеристикам относят объём, размах, моду и среднее измерение.
Объём измерения в данном случае равен 18, так как обрабатывались результаты восемнадцати учеников.
Размах измерения равен 9. Это разница между наибольшим и наименьшим результатами.
Мода измерения — это самый популярный, «модный» результат. В данном случае она равна 3.
Среднее (или среднее арифметическое). Это частное суммы всех результатов измерений на объём измерений.
Чаще всего, как вы понимаете, результатами измерений являются числа. Каждое число, встретившееся в конкретном измерении, называют вариантой измерения.
Если записать все варианты измерений, то получится ряд данных измерения.
Если записать их в порядке возрастания, то получим сгруппированный ряд данных.

Среднюю варианту называют медианой измерения. Если их две, то медиана равна их среднему арифметическому.
В нашем примере средними вариантами являются варианты под номерами 9 и 10. Они обе равны 3, значит, и медиана равна 3.
Определение.
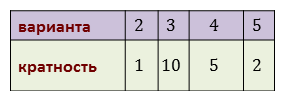
Каждая варианта встречается некоторое число раз, его называют кратностью данной варианты.
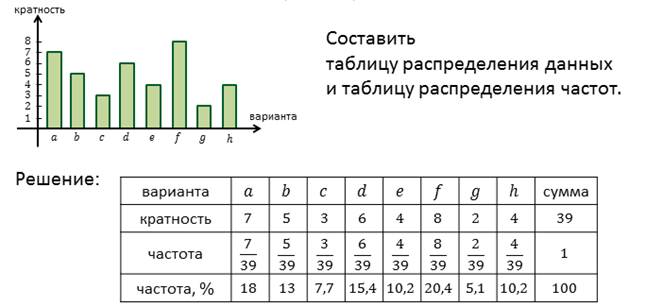
Для нашего примера таблица распределения данных примет такой вид.
Применим полученные знания при решении задачи.
На уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты. Получился такой ряд данных
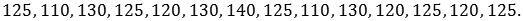
Требуется сгруппировать данные, составить таблицу их распределения, а также найти объём, размах, моду, среднее и медиану измерения.
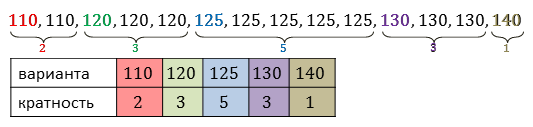
Для начала сгруппируем данные, расположив их в порядке возрастания.
Это позволит нам составить таблицу распределения данных.
Теперь найдём объём измерения.
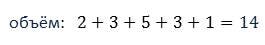
Размах измерения равен разности наибольшей и наименьшей вариант.
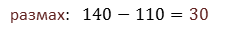
Среднее значение равно частному суммы всех полученных значений и объёма измерения.

Мода измерения равна 125. Ведь это самый популярный результат.
Для отыскания медианы нужно найти среднюю варианту в сгруппированном ряду данных. Их две и обе равны 125. Значит, медиана равна 125. Так мы с вами составили паспорт данных.

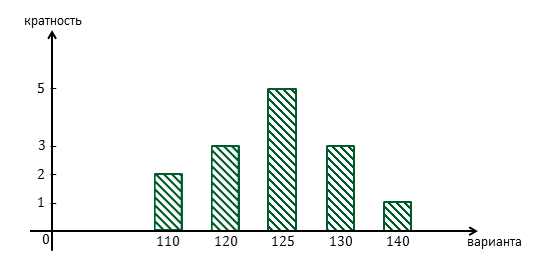
А теперь, по полученной таблице распределения данных построим многоугольник распределения и гистограмму распределения.
Мы имеем 5 вариант: 110, 120, 125, 130 и 140.
Кратность первой варианты равна 2, второй — 3, третьей — 5, четвёртой — 3, и пятой —1.
Соединив полученные точки, получим многоугольник распределения данных.
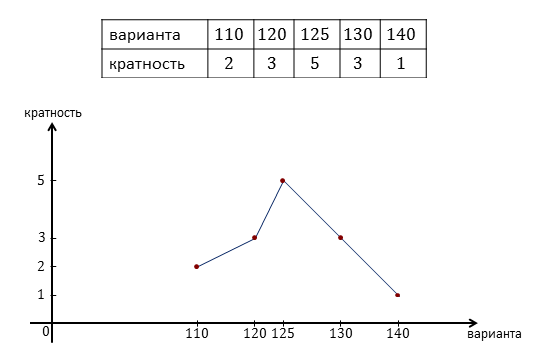
Тогда гистограмма примет такой вид.
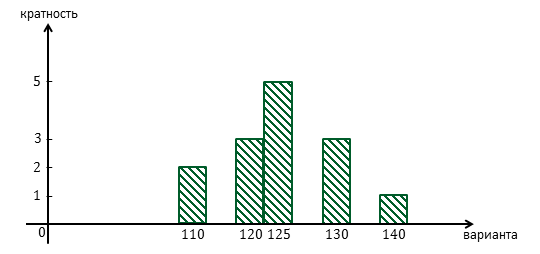
Обратите внимание, варианты могут располагаться неравномерно на оси Ox, между ними могут быть пропуски.
Например, значение 115 не встретилось ни разу, то есть её кратность равна 0. Очевидно, что такое значение не может быть вариантой.
Для построение гистограммы можно было использовать номинативную шкалу, то есть по горизонтали распределить номинации, варианты, а на вертикальной оси оставить значения их кратностей. Гистограмма примет такой вид.
В этом случае вариантами могут быть не только числа.
Если кратность варианты разделить на объём измерения, то получится частота варианты.
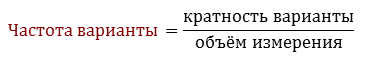
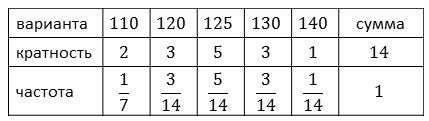
Найдём частоту каждой варианты данной задачи. Обратите внимание, сумма частот всегда равна единице.
Частоту также можно выразить в процентах. Сумма частот в процентах, очевидно, всегда равна 100.
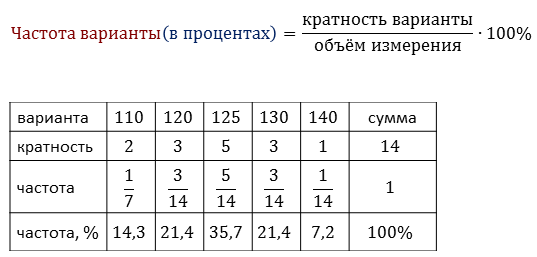
Только что с помощью таблицы распределения данных мы составили таблицу распределения частот.
Выполним задание.
А теперь рассмотрим такой случай.
Пример.

Определение.
Числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией D.
Определение.
Средним квадратическим отклонением называют:
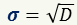
Чем меньше эти значения, тем плотнее группируются данные измерения вокруг среднего значения.
Существует алгоритм вычисления дисперсии данных.
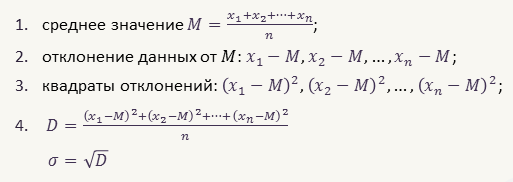
Воспользуемся этим алгоритмом и найдём значение дисперсии результатов отклонения для каждого ружья.
Проведём подсчёты для ружья А. Их удобно производить в таблице.
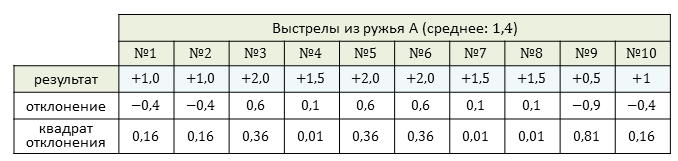
Найдём их среднее значение. Получаем, что дисперсия равна:
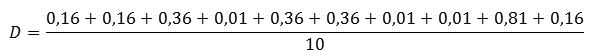
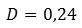
А среднее квадратическое отклонение равно:
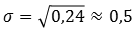
Вычислим значение дисперсии для ружья Б.
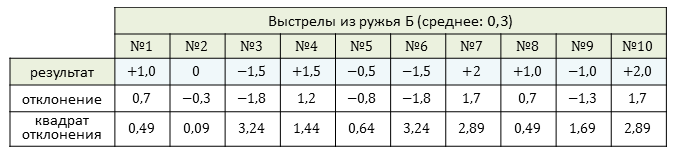
Можем вычислить дисперсию как среднее квадратов отклонений.
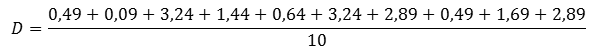
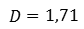
Тогда среднее квадратическое отклонение равно:
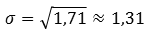
Видим, что дисперсии отличаются практически в 7 раз, а средние квадратические отклонения примерно в 3 раза.
Можно сказать, что ружьё Б стреляет с разбросом в 3 раза большим, чем ружьё А. Поэтому ружьё А точнее.
Подведём итоги нашего урока.
Сегодня вы познакомились и рассмотрели на примерах этапы статистической обработки данных.
Каждое значение, полученное в ходе измерений, мы договорились называть вариантой. А число повторений данной варианты, называют её кратностью.
Вы познакомились с формулой отыскания частоты варианты. И научились составлять таблицу распределения частот.

Также узнали, что числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией.

А ещё, рассмотрели примеры нахождения этих величин с помощью специального алгоритма.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 16806
16806

