Вопросы занятия:
· рассмотрим перпендикулярные плоскости;
· сформулируем и докажем признак перпендикулярности двух плоскостей.
Материал урока.
Для начала давайте вспомним определение двугранного угла. Итак, двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости. Причем, полуплоскости, образующие двугранный угол, называются его гранями. А прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
Введем понятие угла между плоскостями.
Определение. Углом между пересекающимися плоскостями называется угол между прямыми, проведенными в плоскостях перпендикулярно их линии пересечения через некоторую точку.
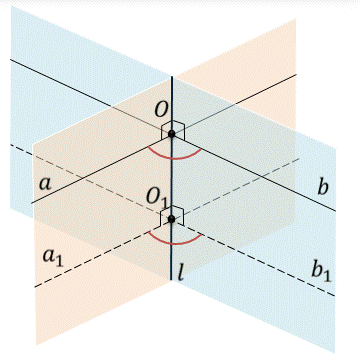
Заметим, что определение угла между плоскостями не зависит от выбора прямых а и b, проведенных в плоскостях и перпендикулярных их линии пересечения. Действительно, если в данных плоскостях провести какие-нибудь другие прямые a1 и b1 перпендикулярно их линии пересечения l через точку O1, то прямая а будет параллельна прямой a1 и прямая b будет параллельна прямой b1. А следовательно, угол между прямыми а и b равен углу между прямыми a1 и b1.
Если
плоскости параллельны, то угол между ними считается равным 0°. Угол между
плоскостями α и β обозначают следующим образом 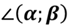 .
.
Если в пространстве пересекаются две плоскости, то они образуют четыре двугранных угла с общим ребром (аналогично как при пересечении двух прямых получаются четыре угла).
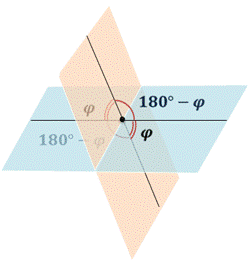
Если известен один из этих двугранных углов, то можно найти и другие три двугранных угла. Т.е. если один из этих двугранных углов равен φ, то другие три угла равны соответственно 180°-φ, φ и 180°-φ.
Если при пересечении плоскостей один из углов прямой (т.е. фи равен 90°), то и остальные три угла прямые. Такие плоскости называют перпендикулярными.
Если φ – тот из четырех углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен φ. Очевидно, что угол φ лежит в промежутке от 0° до 90°.
Определение. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен девяносто градусов.
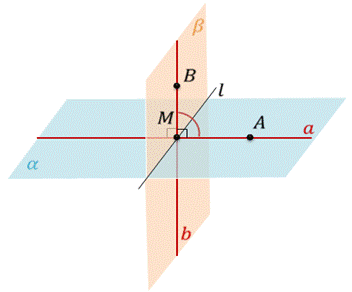
Пусть есть две плоскости α и β, которые пересекаются по прямой l. Отметим произвольную точку М на прямой l. Затем через точку М проведем две прямые а и b перпендикулярные к прямой l в плоскости α и в плоскости β соответственно. На построенных прямых отметим точки А и B соответственно. Обратите внимание, мы получили угол AMB. Угол AMB – это линейный угол двугранного угла. Если угол AMB равен 90°, то плоскости α и β называются перпендикулярными.
Действительно, прямая b перпендикулярна прямой l по построению. Прямая b перпендикулярна прямой а, так как угол между плоскостями α и β равен 90°. Следовательно, прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, прямая b перпендикулярна плоскости α.
Аналогично можно показать, что прямая а перпендикулярна плоскости β. Прямая а перпендикулярна прямой l по построению. Прямая а перпендикулярна прямой b, так как угол между плоскостями α и β равен 90°. Отсюда следует, что прямая а перпендикулярна двум пересекающимся прямым b и l из плоскости β. Значит, прямая а перпендикулярна плоскости β.
Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты.

Ясно, что все четыре двугранных угла, образованные взаимно перпендикулярными плоскостями, прямые.
Теорема. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Доказательство.
Пусть даны плоскости α и β. Причем такие, что плоскость альфа проходит через прямую а, перпендикулярную к плоскости β. Докажем, что плоскости α и β перпендикулярны.
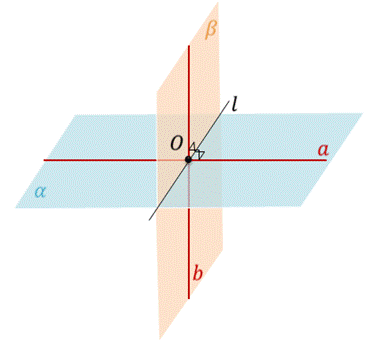
Пусть точка О – точка пересечения прямой а с плоскостью β. Точка О – общая точка плоскостей α и β, следовательно, данные плоскости пересекаются по прямой l, проходящей через точку О.
В плоскости β через точку О проведем прямую b, перпендикулярную прямой l.
Прямые b и l лежат в плоскости β и по условию прямая а перпендикулярна плоскости β. Следовательно, прямая а перпендикулярна прямой b и прямая а перпендикулярна прямой l. Таким образом, получаем, что прямая а лежит в плоскости α, перпендикулярна прямой l и прямая b лежит в плоскости β перпендикулярно прямой l. Значит, угол между плоскостями α и β равен углу между прямыми а и b и равен 90°. Т.е. получили, что плоскости α и β перпендикулярны.
Теорема доказана.
Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Доказательство. Пусть даны две перпендикулярные плоскости α и β, которые пересекаются по прямой l. И дана плоскость γ, которая перпендикулярна линии пересечения плоскостей α и β, т.е. перпендикулярна прямой l. Докажем, что каждая из плоскостей α и β перпендикулярна плоскости γ.
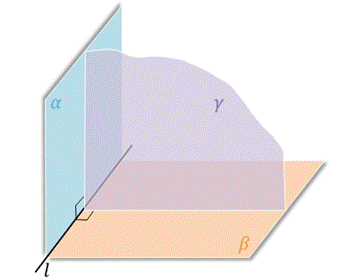
Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.
Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.
Таким образом, получаем, что плоскость α перпендикулярна плоскости γ и плоскость β перпендикулярна плоскости γ.
Что и требовалось доказать.
Второе следствие. Прямая, проведенная в одной из двух перпендикулярных плоскостей перпендикулярно прямой, по которой они пересекаются, перпендикулярна другой плоскости.
Доказательство. Пусть даны две перпендикулярные плоскости α и β, которые пересекаются по прямой l. И дана прямая b, которая лежит в плоскости β и перпендикулярна линии пересечения плоскостей α и β, т.е. перпендикулярна прямой l. Докажем, что прямая b перпендикулярна плоскости α.
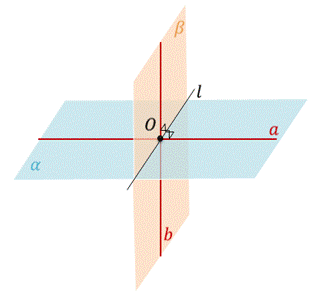
Обозначим буквой О точку пересечения прямой b с прямой l. Затем проведем в плоскости α через точку О прямую а перпендикулярно прямой l. Прямые а и b перпендикулярны прямой l, по которой пересекаются плоскости α и β. Следовательно, угол между прямыми а и b равен углу между плоскостями α и β. Значит, равен 90°.
Таким образом, прямая b перпендикулярна пересекающимся прямым а и l плоскости α. Следовательно, прямая b перпендикулярна плоскости α.
Что и требовалось доказать.
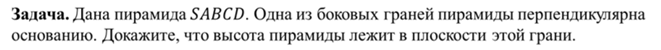
Доказательство.

Что и требовалось доказать.
Подведем итоги урока. На этом уроке мы узнали, что две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен девяносто градусов. Сформулировали и доказали признак перпендикулярности двух плоскостей. А также вывели и доказали некоторые следствия.

 Получите свидетельство
Получите свидетельство Вход
Вход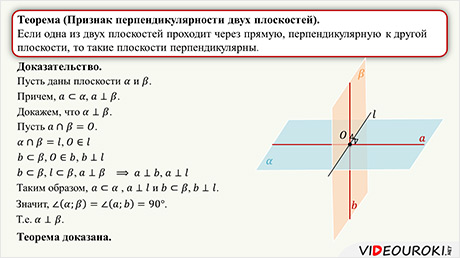



 0
0 16758
16758


