Вопросы занятия:
· введем понятие двугранного угла;
· узнаем о том, как определить линейный угол рассматриваемой геометрической фигуры.
Материал урока.
Для начала давайте вспомним, что понимали под углом в планиметрии. Итак, углом на плоскости мы называлигеометрическую фигуру, образованную двумя лучами, исходящими из одной точки.
В стереометрии наряду с такими углами рассматривается еще один вид углов, которые называют двугранными углами. Но прежде чем мы введем понятие двугранного угла, давайте вспомним одну из аксиом планиметрии: «любая прямая, проведенная в данной плоскости, разделяет эту плоскость на две полуплоскости».
Пусть есть прямая а, которая лежит в некоторой плоскости. Тогда можно указать две части этой плоскости, каждая из которых вместе с прямой а называется полуплоскостью.
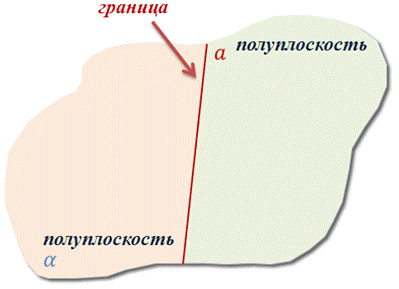
Прямая а называется границей для каждой из полуплоскостей. В отличие от планиметрии, в пространстве две полуплоскости с общей границей прямой а, могут не лежать в одной плоскости.
Давайте представим себе, что мы перегнули плоскость по прямой а так, что две полуплоскости с границей а оказались уже не лежащими в одной плоскости. Полученная фигура и есть двугранный угол.
Определение. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
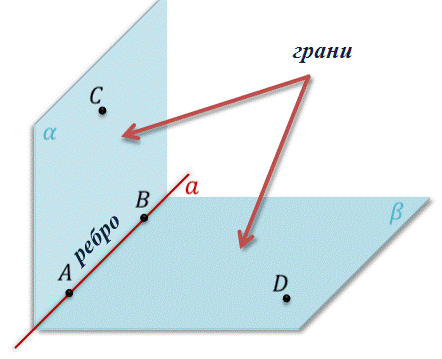
Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани, отсюда и название – двугранный угол.
Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
Двугранный
угол, ребро которого есть прямая AB,
а гранями являются полуплоскости α и β, обозначают так 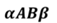 . Обратите внимание, две средние буквы в
обозначении – это ребро данного двугранного угла.
. Обратите внимание, две средние буквы в
обозначении – это ребро данного двугранного угла.
Или, если двугранный угол с ребром AB, на разных гранях которого отмечены точки C и D, то двугранный угол называют CABD.
В обыденной жизни мы часто встречаемся с предметами, имеющими форму двугранного угла. Представление о двугранном угле нам дают: полураскрытая книга, открытый ноутбук, двускатная крыша здания, стена комнаты совместно с полом и т.д.
Напомню, что углы на плоскости измеряются в градусах.
Для измерения двугранного угла вводится понятие линейного угла. Пусть точка О лежит на ребре l двугранного угла. В каждой грани из этой точки проведем лучи ОА и ОB перпендикулярно к ребру l. Угол АОB, сторонами которого служат лучи ОА и ОB, называется линейным углом данного двугранного угла.
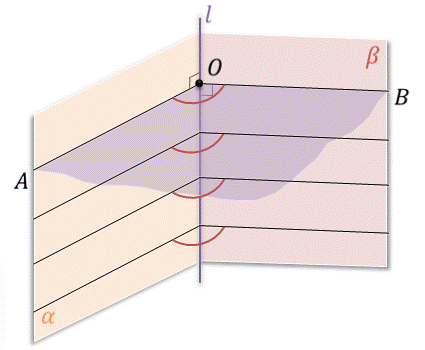
Определение. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
На рисунке вы видите изображение линейного угла AOB двугранного угла с ребром l. Так как ОА перпендикулярно l и ОB перпендикулярно l, то плоскость, в которой лежат лучи ОА и ОB, перпендикулярна к прямой l. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Очевидно, двугранный угол имеет бесконечное множество линейных углов.
Верно следующее утверждение: все линейные углы двугранного угла равны между собой.
Докажем это утверждение.
Рассмотрим два линейных угла А О Б и А один О один Б один двугранного угла,ребро которого эль. Лучи ОА и О один А один лежат в одной грани и перпендикулярны ребру эль. Следовательно, они параллельны. Аналогично и лучи ОБ и О один Б один лежат в одной грани и перпендикулярны ребру эль. Значит, они параллельны.
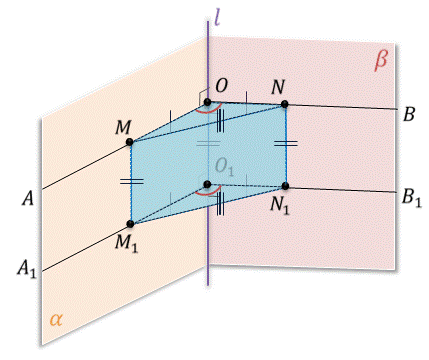
Отложим на лучах ОА и О1A1 равные отрезки OM и O1M1 соответственно, а на лучах ОB и O1B1 – равные отрезки ON и O1N1 соответственно.
Так как OM равно O1M1 и OM параллельно O1M1, то четырехугольник OMM1O1 – параллелограмм. Тогда ОО1 равно MM1 и OO1 параллельно MM1 по свойствам параллелограмма.
Так как ON равно O1N1 и ON параллельно O1N1, то четырехугольник ONN1O1 – параллелограмм. Тогда OO1 равно NN1 и OO1 параллельно NN1 по свойствам параллелограмма. Отсюда, OO1 равно NN1 и OO1 параллельно NN1.
Видим, что тогда MM1 равно NN1 и MM1 один параллельно NN1, т.е. четырехугольник NMM1N1 – параллелограмм. Следовательно, NM равно N1M1.
Рассмотрим треугольники OMN и O1M1N1. Они равны по трем сторонам. Отсюда следует, что угол MON равен углу M1O1N1. А значит, и угол АОB равен углу A1O1B1. Что и требовалось доказать.
Это утверждение можно доказать и быстрее. Достаточно было при рассмотрении линейных углов AOB и A1O1B1 заметить, что так как лучи ОА и O1A1 лежат в одной грани и перпендикулярны к прямой OO1, то они параллельны, а, значит сонаправлены. Точно также лучи ОB и O1B1 лежат в одной грани и перпендикулярны к прямой OO1, следовательно они параллельны, и, значит сонаправлены. Отсюда вытекает, что угол A1O1B1 равен углу AOB (как углы с сонаправленными сторонами). Что и требовалось доказать.
Определение. Градусной мерой двугранного угла называется градусная мера его линейного угла.
Это говорит о том, что, сколько градусов содержится в линейном угле, столько же градусов содержится в его двугранном угле.
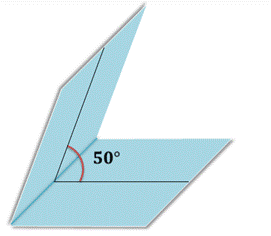
На рисунке вы видите изображение двугранного угла, градусная мера которого равна 50°. Обычно говорят коротко: «Двугранный угол равен 50°».
Различают следующие виды двугранных углов.
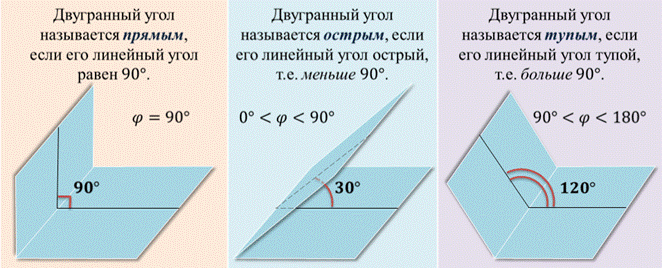
Двугранный угол называется прямым, если его линейный угол равен 90°.
Двугранный угол называется острым, если его линейный угол острый, т.е. < 90° (расположен в промежутке от 0 до 90 градусов).
Двугранный угол называется тупым, если его линейный угол тупой, т.е. > 90° (расположен в промежутке от 90 до 180 градусов).
Если грани двугранного угла лежат в одной плоскости, то он называется развернутым.
В дальнейшем под двугранным углом будем понимать всегда тот, линейный угол φ которого удовлетворяет условию 0°<φ<180°.
Рассмотрим примеры.
Пусть ABCDA1B1C1D1 – прямоугольный параллелепипед. Тогда угол ADD1 является линейным углом двугранного угла, ребро которого есть прямая DC, а его грани – полуплоскости, в которых лежат прямоугольники ABCD и DCC1D1, так как АD перпендикулярно DC и DD1 перпендикулярно DC. Угол ADD1 – прямой, следовательно, указанный двугранный угол – прямой.

Двугранным углом при ребре пирамиды называется двугранный угол, ребро которого содержит ребро пирамиды. А грани двугранного угла содержат грани пирамиды, которые пересекаются по данному ребру пирамиды.
Пусть DABC – правильная треугольная пирамида, а точка О – середина ребра АC. Прямая DО перпендикулярна прямой АС.

Так как медиана в равностороннем треугольнике ABC является и высотой. Прямая BО также перпендикулярна прямой АС. Так как медиана в равнобедренном треугольнике DAC является и высотой. Значит, угол DOB есть линейный угол двугранного угла DACB, ребро которого – прямая AC, а гранями являются полуплоскости, содержащие треугольники ABC и DAC.
Подведем итоги урока. На этом уроке мы познакомились с понятием двугранного угла. Узнали, что двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости. Ввели понятие линейного угла: линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру. А также убедились, что градусной мерой двугранного угла называется градусная мера его линейного угла и, что все линейные углы двугранного угла равны между собой.

 Получите свидетельство
Получите свидетельство Вход
Вход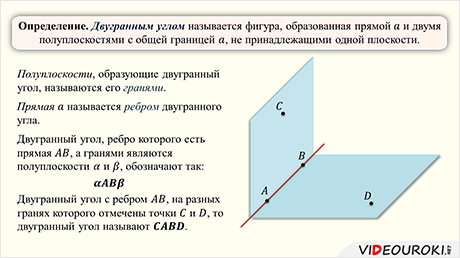



 0
0 15452
15452