На этом уроке мы с вами изучим этапы разработки программы решения задачи. А также опишем с их помощью пример.
При решении задачи существует несколько этапов:
1. Постановка задачи;
2. Формализация задачи;
3. Анализ математической задачи;
4. Построение алгоритма;
5. Составление программы и тестирование.
Давайте рассмотрим их более подробно на примере следующего равенства:
|a| · x = 3.
a – вводится с клавиатуры.
Начнём с постановки задачи. Нам нужно найти решение равенства, то есть x. Таким образом, на этапе постановки задачи нужно:
· понять условие задачи;
· выделить исходные и результирующие данные;
· понять отношения между ними.
Можно сказать, что нам нужно ответить на вопросы:
· Что нужно найти по условию задачи? В нашем случае нужно найти x.
· Что при этом дано? Дано значение a.
· Чем можно пользоваться при решении задачи? При решении нужно из равенства вывести значение x.
Далее идёт этап формализации задачи. На этом этапе необходимо оформить описательную информационную модель при помощи какого-либо формального языка, чаще всего с помощью математического. То есть, на этом этапе мы должны записать формулы, с помощью которых мы сможем в дальнейшем решить задачу исходя из исходных данных и результата, который необходимо получить. То есть наше x будет равно следующему выражению:
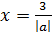 .
.
После того, как мы записали задачу на математическом языке, нужно её проанализировать. Это нам необходимо для того, чтобы составить правильный алгоритм решения, обладающий всеми свойствами алгоритма.
Рассмотрим, к каким результатам могут привести различные исходные данные переменной a.

Перейдём к этапу построения алгоритма.
Для этого будем использовать блок-схему. Прежде, чем приступить к составлению блок-схемы, давайте вспомним правила:
· каждая базовая структура должна иметь один вход и один выход;
· блок-схема должна изображаться при помощи стандартных элементов.
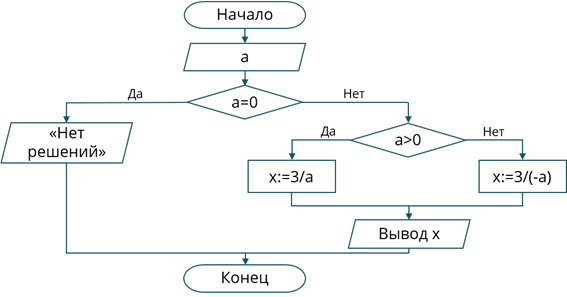
В начале нам нужно нарисовать блок ввода переменной a. Далее идёт проверка a. Если условие a = 0 истинно, то на экран выведем сообщение, что «Нет решений». Если же условие ложно, то снова будет идти блок условия, в котором проверим следующее: a > 0. Если условие истинно, то x = 3/a. Если условие ложно, то x = 3/ (–a). После проверки этого условия будет идти блок вывода значения x. Конец программы.
Алгоритмический язык – это язык описания алгоритмов с русскими служебными словами.
Прежде, чем строить алгоритм на учебном Алгоритмическом языке, вспомним правила:
· конструкции одного уровня вложенности записываются на одном вертикальном уровне;
· вложенная конструкция записывается смещённой по строке на несколько позиций вправо относительно внешней для неё конструкции.
Наш алгоритм будет выглядеть следующим образом:

Если обратить внимание. То можно заметить, что наш алгоритм записан по всем правилам как в блок-схеме, так и на алгоритмическом языке, поэтому его чтение не составит труда и не даст возможности запутаться в конструкциях.
После того, как мы с вами записали алгоритм на учебном Алгоритмическом языке, можно приступать непосредственно к составлению программы на языке Pascal. Следует помнить, что при написании программы на языке Pascal необходимо соблюдать такие же правила, как и при записи алгоритма на учебном Алгоритмическом языке.
Запишем следующее:
program prim;
Далее объявим переменные a, x вещественного типа.
begin
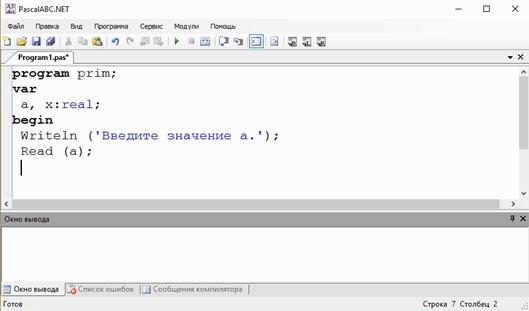
Организуем диалог между компьютером и пользователем:
Writeln (‘Введите значение a ');
Считаем её при помощи функции Read и присвоим соответствующей переменной.
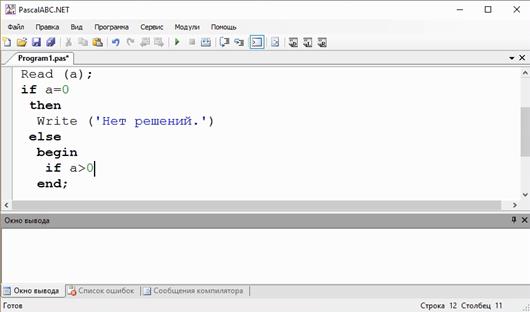
Далее идёт первый условный оператор, в котором проверяем следующее: a = 0. Если условие истинно, то запишем вывод на экран сообщения «Нет решений», так как наше неравенство не будет иметь решения.
Если условие ложно, запишем else, а затем открываем и закрываем операторные скобки при помощи служебных слов begin, end. При написании программы если нам необходимо использовать операторные скобки, то лучше всего, после открытия, сразу же закрыть, чтобы в дальнейшем не путаться, так как операторных скобок может быть в программе большое количество.
Итак, если условие ложно, то после слова begin снова будет идти условие, в котором будет проверяться следующее: a > 0.
Если это условие истинно, то x:=3/a. Если же условие a > 0 ложно, то после else x:=3/(–a). Оформим вывод на экран x при помощи функции Write.
Так как у нас операторная скобка уже закрыта, переходим на строку ниже после end.
Завершим программу.
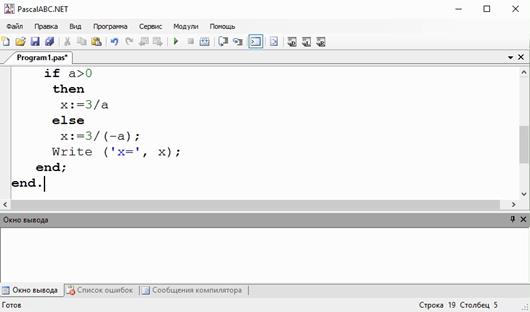
При написании и вводе в компьютер больших программ существует вероятность совершения синтаксических ошибок. Синтаксические ошибки – это ошибки, которые нарушают правила грамматики языка. Соответственно, программисту нужно найти и исправить эти ошибки. Таким образом, отладка – это поиск и устранение синтаксических ошибок. При выполнении программы, если была обнаружена ошибка, система программирования не только выдаст сообщение об ошибке, но и укажет строку, в которой она находится.
Заключительным этапом построения программы решения задачи является тестирование.
Тестирование – это этап, на котором экспериментально доказывается правильность алгоритма, заключённого в программе, и работоспособность программы.
Тест – это вариант решения задачи с заданными исходными данными, для которых известен результат.
Прежде, чем приступать к тестированию, следует составить план. Для ветвящегося алгоритма необходимо проверить все его ветви. Так как у нас 3 ветви, то у нас должно быть как минимум 3 варианта ответа.
Начнём с простого. Если a = 0, то ответом должно быть «Нет решений».

Проверим.
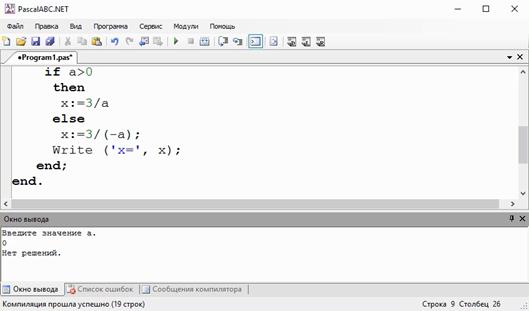
Эта ветвь работает верно.
Далее при a > 0, x = 3/a. Для простоты вычисления возьмём a = 3. То есть x=1.

Проверим.
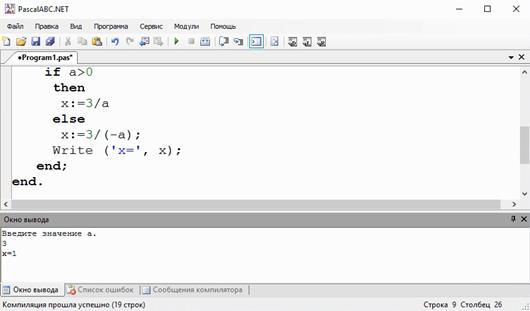
И снова мы получаем верный результат.
Проверим заключительную ветвь, если a < 0. Снова возьмём для простоты вычислений число –3. Вычислим x: 3/(-(-3)) = 0.

Проверим нашу программу.
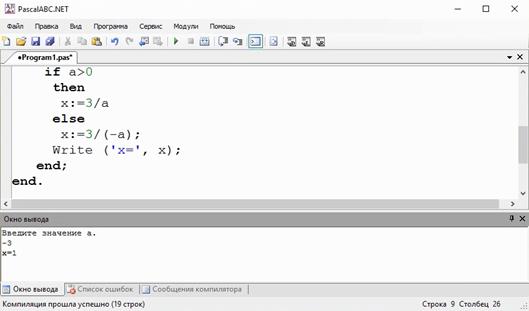
Мы получили верный ответ.

При анализе результатов тестирования можно сделать следующий вывод: правильность алгоритма и работоспособность программы доказана.
Пришла пора подвести итоги урока.
Вспомним ещё раз, что в себя включает каждый этап решения задачи.
Итак, на этапе постановки задачи происходит определение исходных данных и искомых результатов.
На этапе формализации происходит переход к задаче обработки некоторой знаковой системы, например, к математической задаче.
При анализе математической задачи необходимо определить все варианты множеств значений исходных данных, а также определить для каждого варианта способ решения и вид выходных данных (результатов).
При построении алгоритма нужно определить структуру алгоритма и последовательности команд. После чего представить алгоритм на каком-либо языке описания алгоритмов. Например, в виде блок-схемы или же на учебном Алгоритмическом языке.
На этапе составления программы происходит запись и отладка программы на языке программирования. Необходимо строго соблюдать правила синтаксиса языка.
И заключительный этап – тестирование. На этом этапе происходит экспериментальное доказательство правильности алгоритма и работоспособности программы. В свою очередь, тест – это варианты решения задачи с заданными исходными данными, для которых известен результат. Так же на этом этапе необходимо построить план тестирования таким образом, чтобы наиболее полно проверить работу программы.

 Получите свидетельство
Получите свидетельство Вход
Вход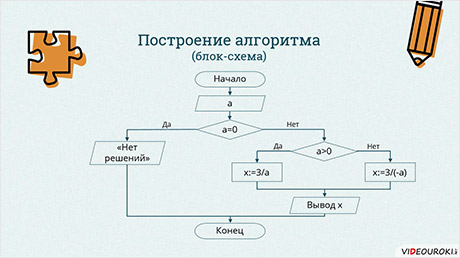




 6789
6789

