На этом уроке мы с вами вспомним, как записывается условный оператор и оператор выбора на языке программирования Pascal, а также решим несколько задач с использованием этих структур.
В начале урока давайте вспомним, что такое ветвление.
Ветвление – это алгоритмическая конструкция, при помощи которой происходит выбор одной из двух серий действий с выходом на общее продолжение. Давайте рассмотрим блок-схему полного ветвления.

Исходя из неё, мы видим, что, если условие является истинным, то выполняется серия 1, если же нет, то серия 2. Условие, в данном случае, это утверждение, которое может быть либо истинным, либо ложным. То есть условие – это логическое выражение. Теперь рассмотрим блок-схему неполного ветвления.
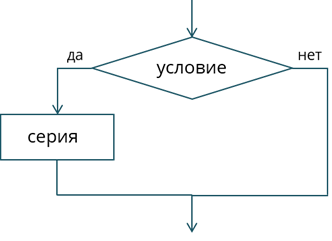
Если условие истинно, то выполняется серия, а если нет, то ничего не происходит.
В языке программирования Pascal такая структура записывается следующим образом:

В полной форме, если логическое выражение истинно, то выполняется оператор 1 (после then), в обратном случае – оператор 2 (после else).
В неполном ветвлении если логическое выражение истинно, то выполняется оператор, а если ложно, то программа переходит к следующей команде.
Обратите внимание, что при записи оператора ветвления в алгоритм, после «Если» используется условие, а вот при записи на языке программирование, будет записано логическое выражение, которое вычисляется в первую очередь.
В качестве оператора может быть, как одна команда, так и несколько. В случае, если команд несколько, стоит заключать их в операторные скобки begin…end.
А сейчас давайте напишем несколько программ.
Пример 1. Написать программу, исходя из следующего условия: Положение фигуры на шахматной доске описывается двумя числами – номером горизонтали и номером вертикали. Ввести с клавиатуры координаты ферзя (x, y) и координаты любой фигуры (m, n). Проверить, находится ли фигура под ударом. Ферзь бьёт по вертикали, горизонтали и диагонали. Координаты ферзя и пешки не должны совпадать.
Прежде, чем составлять программу, давайте разберёмся при помощи рисунка.

Итак, у нас изображена шахматная доска. Пусть ферзь будет находится в клетке с координатами (4, 2).
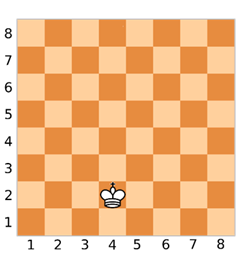
Нарисуем прямые линии, по которым может ходить ферзь. То есть нарисуем горизонтальную, вертикальную и две диагональных линии.
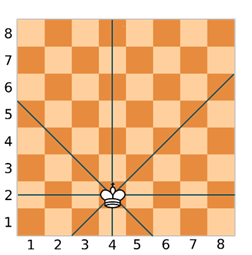
Давайте возьмём любую фигуру, например, пешку, и поставим её, например, в клетку, с координатами (5, 2).
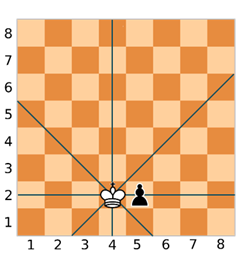
Мы можем видеть, что наша фигура находится под ударом. Помимо этого, у ферзя и пешки совпадают вторые точки координат, то есть y = n. Это будет первым условием, когда фигура будет находиться под ударом ферзя по горизонтали.
По вертикали фигура будет находится под ударом в том случае, если у ферзя и пешки будут совпадать первые точки координат, то есть если x = m. Давайте поставим пешку в клетку с координатами (4, 3).
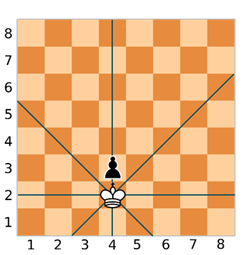
Мы видим, что она находится под ударом. Это будет вторым условием.
Ферзь ещё может ходить по диагонали. Здесь также есть своя закономерность для того, чтобы узнать, находится ли фигура под ударом. Для этого нужно сравнить модули разности x–m и y–n. Если они равны, то фигура находится под ударом ферзя.
|x–m| = |y–n|
Давайте проверим. Поставим пешку в клетку с координатами (5, 3). Как мы помним, ферзь стоит в клетке с координатами (4, 2).
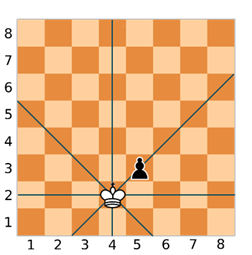
Вычислим |x–m|. Он будет равен 1. Также вычислим |y–n|. Он будет также равен 1. Соответственно модули разности равны, и фигура находится под ударом.
Теперь давайте проверим другую диагональ. Поставим фигуру в клетку с координатами (5, 1).
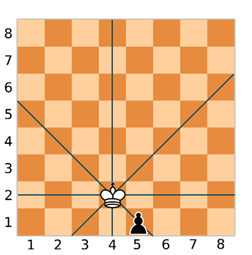
При вычислении модулей разности получим, что они равны 1. Соответственно фигура снова находится под ударом.
А сейчас давайте перейдём непосредственно к написанию программы.
Зададим имя программы z1, то есть задание 1. Далее объявим 4 переменных x, y, m, n целого типа integer.
После слова begin организуем диалог между пользователем и компьютером. Пишем Write, а в скобках и одинарных кавычках попросим ввести координаты для ферзя (x, y). Присвоим соответствующим переменным значения, введённые с клавиатуры при помощи операции Read.
Аналогично поступим и с вводом с клавиатуры координат для фигуры. Скопируем две функции Write и Read и изменим их для ввода данных новой фигуры. В операторе Read считаем значения переменным m и n.
Теперь нам нужно записать условие. Мы с вами помним, что у нас 3 логических выражения и, при выполнении хотя бы одного из них, наша фигура будет находится под ударом. Поэтому запишем их при помощи дизъюнкции, то есть будем использовать союз or.
Далее идёт служебное слово then В случае, если хотя бы одно из условий выполняется, наша фигура будет находится под ударом. Значит здесь мы должны вывести соответствующее сообщение:
Write (‘Фигура находится под ударом’)
Точку с запятой в конце не ставим, так как мы с вами будем использовать полную форму ветвления, а перед else точка с запятой не ставятся.
Пишем слово else. Так как после else пишутся команды, которые будут выполнятся только в том случае, если ни одно из условий не выполняется, то здесь мы должны вывести на экран строку, в которой будет говориться, что фигура не попадает под удар. То есть мы должны записать следующее:
Write (‘Фигура не находится под ударом’)
Завершаем нашу программу.

Для проверки будем использовать координаты, которые мы с вами проверяли при помощи рисунка.
Итак, координаты ферзя – (4, 2). Координаты пешки – (5, 2).

Фигура находится под ударом.
Далее введём всё те же координаты для ферзя, а для пешки зададим координаты (5, 3).

И снова получаем верный результат.
А сейчас давайте возьмём координаты, при которых пешка не будет находится под ударом. Например, (6, 1).

И снова мы получили верный результат. Значит задача решена верно.
Рассмотрим ещё один пример. Составить блок-схему и написать программу для решения геометрической задачи. Определите, является ли треугольник со сторонами a, b, c равнобедренным. Если да, то укажите, что является основанием, а что – боковыми сторонами.
Прежде чем приступать к решению, давайте вспомним, что такое равнобедренный треугольник. Равнобедренный треугольник – это треугольник, в котором две стороны равны между собой. Таким образом, если наш треугольник равнобедренный, то a должно быть равно b, или же a равно c, или b равно c.
Давайте составим блок-схему.
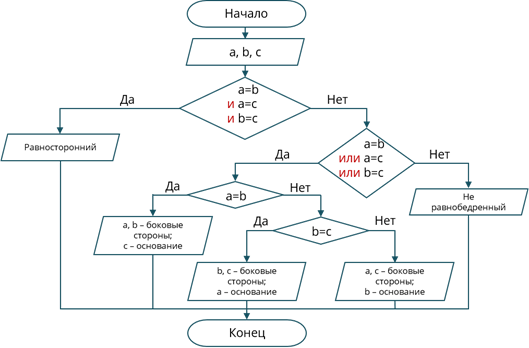
Начало. Затем идёт ввод переменных a, b и c. Далее идёт блок условия, в котором мы будем проверять, равны ли все 3 стороны между собой. Если да, то треугольник является равносторонним и соответственно будет идти блок вывода на экран соответствующей информации. Если же 3 стороны не равны между собой, то будет снова идти блок условия, в котором будет проверятся, равны ли между собой хотя бы 2 из сторон. Если нет и все 3 стороны разные, то будет идти блок вывода информации, что треугольник не является равнобедренным. Если же условие будет выполняться, то снова будет идти блок условия, в котором будем проверять следующее: a = b. Если да, то будет идти блок вывода на экран со следующим сообщением: a и b – боковые стороны треугольника, c – основание. Если же условие a = b ложно, то будет идти очередной блок условия, в котором будет проверять следующее: b = с. Если условие истинно, то будет идти блок вывода информации со следующим текстом: b, c –боковые стороны треугольника, a – основание. Если условие b = c – ложно, то будет идти блок вывода информации: a, c – боковые стороны треугольника, b – основание.
В конце от всех блоков вывода информации будут идти линии к блоку конца программы.
А сейчас давайте напишем программу.
Объявляем 3 переменных a, b, c вещественного типа, так как стороны треугольника могут быть равны вещественным числам. После begin Выведем на экран следующее сообщение: «Введите три стороны треугольника через пробел в следующем порядке: a, b, c.». Функцией Read зададим соответствующим переменным введённые значения. Далее будет идти условный оператор if, с помощью которого мы с вами проверим, равны ли все 3 стороны между собой. Это будет записано так:
(a = b) and (a = c) and (b = c)
Если условие истинно, то после then будет идти операция вывода:
Write (‘Треугольник является равносторонним’)

Если же условие ложно, то после else будет идти ещё один условный оператор if, в котором мы проверим, равны ли между собой хотя бы две стороны треугольника. Запишем then и перейдём на новую строку.
else. Давайте сначала запишем, что будет, если условие ложно. То есть после else запишем функцию
Write (‘Треугольник не является равнобедренным.’);
Вернёмся к условию. Если 2 стороны треугольника равны, то нужно выяснить какие, поэтому после then запишем условный оператор, при помощи которого проверим следующее: a = b. Если условие истинно, то после then пишем функцию
Write (‘a, b – боковые стороны треугольника, c – основание.’)
Если условие a = b ложно, то снова при помощи условного оператора if проверим стороны b и c.
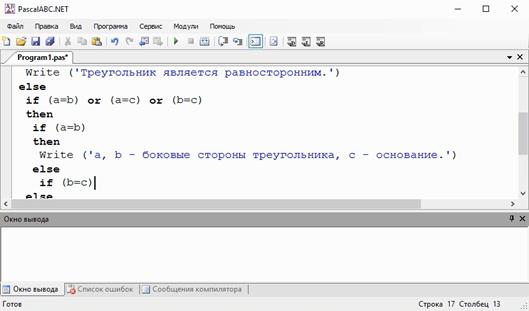
Если они равны, то на экран будет выводиться сообщение
Write (‘b, c – боковые стороны треугольника, a – основание.’)
Если условие b = c – ложно, то на экран снова выведем сообщение
Write (‘А, Цэ – боковые стороны треугольника, Бэ -основание.’);
Нам осталось завершить программу. Пишем в конце end с точкой.

А теперь давайте проверим программу. Запускаем её и введём три единицы.

Такой треугольник является равносторонним, и мы получили соответствующее сообщение от программы.
А сейчас проверим, если все стороны не равны.
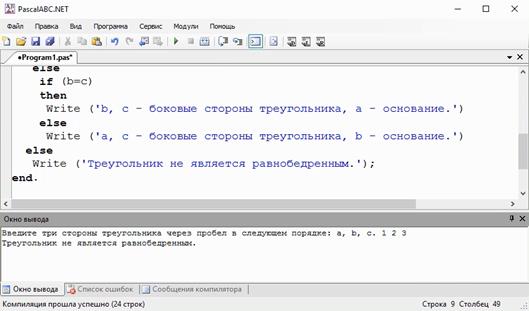
На экран выводится сообщение о том, что треугольник не является равнобедренным.
А сейчас поочерёдно проверим случаи, если a = b, b = c и a = c.



Программа работает верно.
В языке программирования Pascal существует оператор выбора case. Рассмотрим его формат записи в полной и неполной формах:

В этих записях «селектор» – это выражение любого порядкового типа; «константа» – постоянная величина того же типа, что и «селектор»; «оператор» – любой простой или составной оператор.
Давайте разберёмся на примере. Преобразовать введённое целое число из диапазона от 1 до 5 в его словесное представление.
Этот пример можно решить двумя способами: при помощи условного оператора или же оператора выбора.
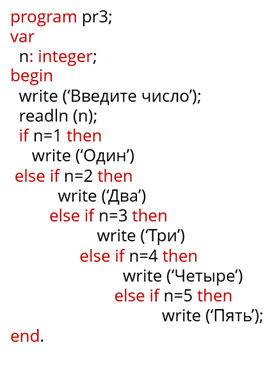
Мы видим, что писать такую программу при помощи условного оператора скучно и однообразно. Давайте напишем эту же программу с использованием составного оператора.
Итак, начало программы будет таким же, как и при использовании условного оператора, включая функцию Read. Далее будет идти оператор case n of. Запишем все варианты наших чисел. Если введено число 1, то на экране должно появиться соответствующее сообщение. Записывается следующим образом:
1: Write (‘Один’);

Таким же образом расписываются и остальные 4 варианта.
Если же введено число, не входящее в наш диапазон, то выведем сообщение, в котором будет указано, что введено другое число. То есть после else запишем функцию Write и соответствующий текст. Завершим оператор выбора словом end и точка с запятой. После этого завершим всю программу.

Запустим её и проверим.


Программа работает верно.
А теперь давайте разберёмся, как она работает.
Сначала вычисляется выражение-селектор, то есть программа смотрит, чему равно n. Далее в списках констант ищется такое значение, которое совпадает с полученным значением селектора, то есть ищет число, равное n. После этого выполняется оператор, помеченный данной константой. В нашем случае выводится на экран словесное представление числа. Если же такой константы нет, то происходит переход к выполнению оператора, следующего после слова else. То есть если, введено число, не принадлежащее к нашему диапазону, то на экран будет выведено сообщение, что введено другое число.
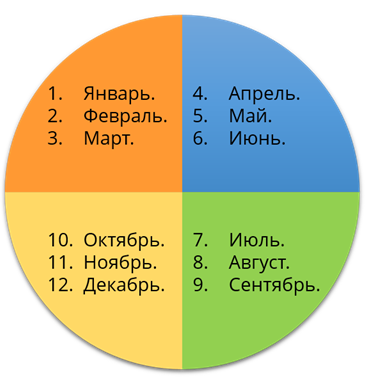
Давайте составим программу, исходя из следующего условия: определить номер квартала по введённому номеру месяца.
Прежде чем приступать к написанию программы, давайте вспомним, что в году 4 квартала. В каждом квартале по 3 месяца. То есть первый квартал включает в себя первый, второй и третий месяца; Второй – четвёртый, пятый и шестой месяца; и так далее.
Приступим к написанию программы.
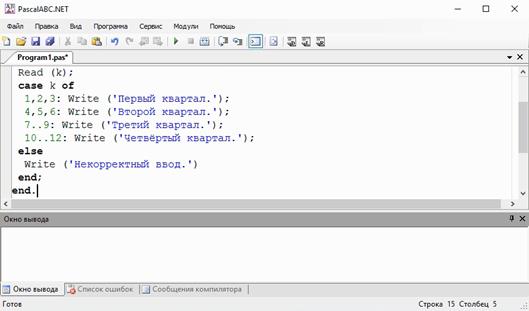
Объявим переменную k целого типа. Далее, после begin, организуем диалог между пользователем и компьютером и попросим ввести номер месяца. Считаем его при помощи функции Read. Теперь запишем сам оператор выбора: case k of.
Далее перечислим номера первый трёх месяцев через запятую, а после двоеточия запишем функцию вывода
Write (‘Первый квартал.’);
На следующей строчке пишем номера месяцев, которые входят во второй квартал и выводим на экран соответствующий текст.

Далее запишем следующее:
7..9: Write (‘Третий квартал’);
Такая запись указывает диапазон чисел. В нашем случае в него будут входить числа 7, 8 и 9.
Запишем аналогичным образом строку для 4 квартала.
После else у нас будет идти оператор вывода со следующим текстом
Write (‘Некорректный ввод.’);
Завершим оператор вывода:
end;
Завершим всю программу.
Проверим её.

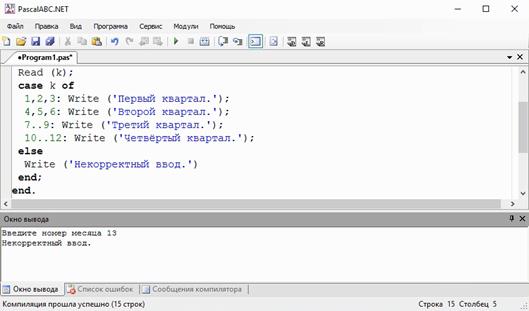
Программа работает верно.
Пришла пора подвести итоги урока. Сегодня мы с вами вспомнили как выглядят и работают условный оператор и оператор выбора. Также решили несколько задач с использованием этих операторов.

 Получите свидетельство
Получите свидетельство Вход
Вход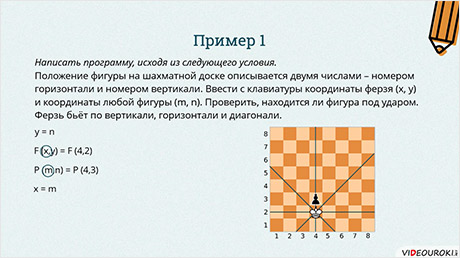




 6096
6096