Сегодня на уроке мы вспомним правило произведения. Вспомним, что называют перестановками. Выясним, какие соединения называют размещениями. Выведем формулу для вычисления числа размещений.
Прежде чем приступить к рассмотрению новой темы, вспомним правило
произведения. Итак, если существует  вариантов
выбора первого элемента и для каждого из них имеется
вариантов
выбора первого элемента и для каждого из них имеется  вариантов
выбора второго элемента, то всего существует
вариантов
выбора второго элемента, то всего существует  различных
пар с выбранными таким образом первым и вторым элементами.
различных
пар с выбранными таким образом первым и вторым элементами.
Это правило может быть применено неоднократно для подсчёта числа соединений из трёх, четырёх, пяти и так далее элементов, выбираемых из определённых множеств с конечным числом элементов.
Перестановками из 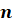 элементов называются соединения, которые состоят из одних и тех же
элементов называются соединения, которые состоят из одних и тех же  элементов и
отличаются одно от другого только порядком их расположения. Число перестановок
из
элементов и
отличаются одно от другого только порядком их расположения. Число перестановок
из  элементов
находят по формуле:
элементов
находят по формуле: 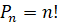 . Напомним,
что
. Напомним,
что  факториал –
это произведение первых
факториал –
это произведение первых  натуральных
чисел.
натуральных
чисел.
Перестановки – это простейшие комбинации, которые можно составить из элементов конечного множества.
А теперь давайте выясним, сколько различных двузначных чисел можно
записать с помощью цифр 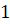 ,
, 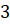 ,
,  ,
, 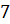 при условии,
что в каждой записи нет одинаковых цифр?
при условии,
что в каждой записи нет одинаковых цифр?
Итак, если на первое место двузначного числа поставить цифру 1, то на второе место можно поставить цифру 3, цифру 5, цифру 7. Если на первое место двузначного числа поставить цифру 3, то на второе место можно поставить цифру 1, цифру 5, цифру 7. Если на первое место двузначного числа поставить цифру 5, то на второе место можно поставить цифру 1, цифру 3, цифру 7. Если на первое место двузначного числа поставить цифру 7, то на второе место можно поставить цифру 1, цифру 3, цифру 5.

У нас получилось 12 двузначных чисел.
Мы перебором установили, что из четырёх данных цифр можно составить 12 двузначных чисел при условии, что в каждой записи числа нет одинаковых цифр.
На одном из предыдущих занятий мы с вами решали такие задачи. Так,
в качестве первой цифры двузначного числа может быть выбрана любая из цифр 1, 3,
5, 7. А в качестве второй цифры может быть выбрана любая из оставшихся трёх
цифр. Тогда по правилу произведения число всевозможных двузначных чисел,
удовлетворяющих условию задачи, равно  , то есть
равно 12.
, то есть
равно 12.
Отметим, что при решении задачи из четырёх данных элементов (цифр 1, 3, 5, 7) были образованы всевозможные соединения по два элемента в каждом. При этом любые два соединения отличались либо составом элементов, либо порядком их расположения.
Например, числа 35 и 37 отличаются составом элементов, а числа 35 и 53 – расположением элементов. Такие соединения называют размещениями.
Сформулируем определение. Размещениями из 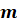 элементов
по
элементов
по 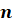 элементов (
элементов (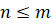 ) называются
такие соединения, каждое из которых содержит
) называются
такие соединения, каждое из которых содержит  элементов,
взятых из данных
элементов,
взятых из данных  разных
элементов, и которые отличаются одно от другого либо самими элементами, либо
порядком их расположения.
разных
элементов, и которые отличаются одно от другого либо самими элементами, либо
порядком их расположения.
Число всевозможных размещений из  элементов по
элементов по
 элементов
обозначают
элементов
обозначают 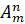 . Читают: «А
из ЭМ по ЭН». Например, в предыдущей задаче было установлено, что
. Читают: «А
из ЭМ по ЭН». Например, в предыдущей задаче было установлено, что 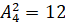 .
.
Сейчас мы с вами выведем формулу для вычисления числа размещений
из  элементов по
элементов по
 элементов.
элементов.


Например, 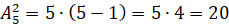 ,
,
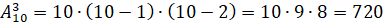 ,
,

Отметим, что правая часть формулы содержит произведение  последовательных
натуральных чисел, наибольшее из которых равно
последовательных
натуральных чисел, наибольшее из которых равно  .
.
Если в этой формуле 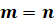 , то она
примет вид:
, то она
примет вид:

 .
.
То есть число размещений из  элементов по
элементов по
 равно числу
перестановок из этих элементов.
равно числу
перестановок из этих элементов.
Давайте выясним, сколькими способами можно обозначить вершины
данного треугольника, используя буквы 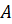 ,
, 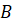 ,
, 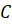 ,
,  ,
, 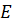 ,
,  ?
?
Для обозначения вершин треугольника используют, как правило, три заглавные латинские буквы.
Чтобы ответить на вопрос задачи, надо найти число размещений из 6 элементов по 3 элемента в каждом. Тогда воспользуемся формулой и получим:
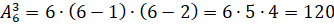 .
.
Таким образом, 120 способами можно обозначить вершины данного треугольника, используя данные буквы.
Теперь решим уравнение  относительно
относительно
 .
.
Заметим, что здесь 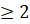 и
и 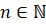 .
.

Сейчас преобразуем формулу  для
нахождения числа размещений из
для
нахождения числа размещений из  элементов по
элементов по
 элементов.
элементов.

Для того чтобы полученная формула была справедлива не только для  , но и для
, но и для  , полагают
, полагают  .
.
Давайте с вами вычислим 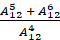 .
.

Задание первое. Вычислите:
а) 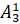 ; б)
; б) 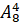 ; в)
; в) 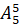 ; г)
; г) 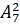 .
.
Решение.

Задание второе. Сколькими способами из 30 учеников класса могут быть выбраны староста и редактор стенгазеты?
Решение.

Задание третье. Найдите значения выражений:
а) 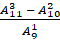 ; б)
; б)  .
.
Решение.

Задание четвёртое. Решите
уравнение  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 1767
1767

