Получите свидетельство
Вход
Начнём с повторения уже известных нам сведений о прямоугольном треугольнике.
Прямоугольным называется треугольник, у которого один из углов прямой.
Сторону, лежащую против прямого угла, называют гипотенузой, а две другие — катетами.
Вы уже знакомы с очень важной теоремой, теоремой Пифагора. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
А также вам известны признаки равенства прямоугольных треугольников. Они могут быть равны: по двум катетам, по катету и прилежащему к нему углу, по гипотенузе и острому углу, по катету и гипотенузе.
Сегодня поговорим о пропорциональных отрезках в прямоугольном треугольнике. И начнём с задачи.
Задача. Докажите, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Доказательство.
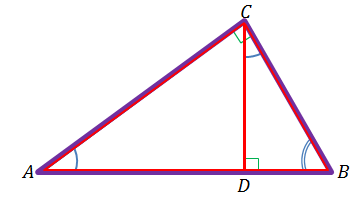
1. 
2. 
3. 
Так мы доказали, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых, в свою очередь, подобен данному треугольнику.
Определение.
Отрезок 
называется
средним пропорциональным
(или средним геометрическим) для отрезков 
и
,
если 
.
Опираясь на данное определение и задачу, решённую нами, докажем следующие утверждения:
высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
В предыдущей задаче нами уже было доказано, что треугольники
катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Докажем второе утверждение.
Для этого воспользуемся подобием треугольников ABC и ACD. Запишем отношение соответствующих сторон.
Отсюда получаем, что АЦ равно корню квадратному из произведения АБ и АД.
Выполним задание.
Задача. Найдите элементы прямоугольного треугольника по известным данным.
а) 
б) 
в) 
г)
Решение.
а) 
б) 
в) 
г)
Задача. По данным
рисунка нужно найти площадь 
.
Решение.
а) 
1. 
2. 
3. 
б) 
1. 
2. 
3. 
4. 
Ответ: а) 
, б) 
.
Задача. 
—
ромб, 
равно
12, 
.
Найдите площадь ромба.
Решение.
1. 
2. Пусть 
3. 
4. 
Ответ: 
.
Подведём итоги урока.
Сегодня вы познакомились с определением среднего геометрического и узнали, как это понятие связано с прямоугольным треугольником.
А именно:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
0
29595
