В прошлой теме говорилось о таком понятии как импульс тела, который является одним из фундаментальных понятий классической механики.
Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость, а направление вектора импульса совпадает с направлением вектора скорости.
Теперь перейдем к следующему важному вопросу — закону сохранения импульса.
Рассмотрим систему трех тел. На тела действуют внешние силы 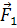 ,
, 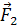 и
и 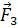 .
.
Силы 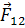 ,
, 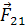 ,
, 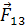 ,
, 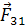 ,
, 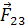 и
и 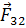 — это внутренние силы.
— это внутренние силы.
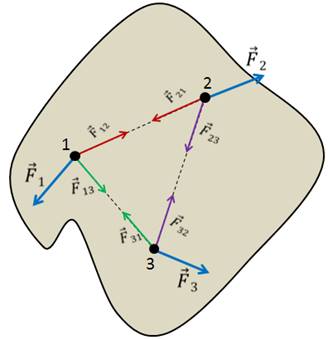
Запишем для каждого тела основное уравнение динамики.
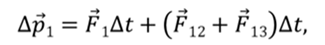
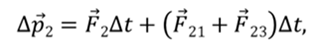

Просуммировав эти уравнения, учтя третий закон Ньютона, получим:


Последняя формула представляет собой импульс системы.
Таким образом, импульс системы тел равен геометрической сумме импульсов тел системы.
Рассмотрим следующий опыт с «колыбелью Ньютона».
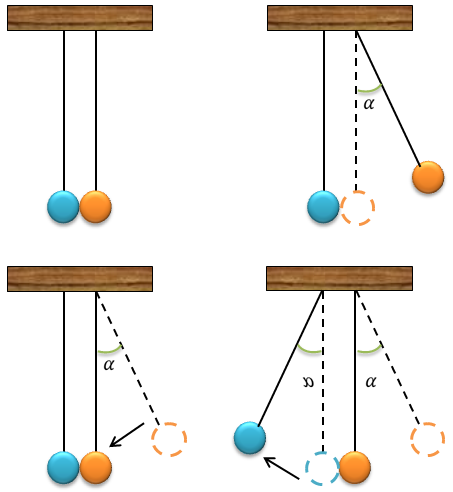
Крайний шарик отклоняют от вертикали на угол a и отпускают. Вернувшись в прежнее положение, он ударяет по шарику и останавливается. При этом шарик с другого конца приходит в движение и отклоняется на тот же угол a. В данном случае очевидно, что в результате взаимодействия шаров импульс каждого из них изменился: насколько уменьшился импульс правого шара, настолько же увеличился импульс левого.
Если два или несколько тел взаимодействуют только между собой (т.е. не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.
Импульс каждого из тел, входящих в замкнутую систему, может меняться в результате их взаимодействия друг с другом. Но векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел. В этом заключается закон сохранения импульса. Этот закон справедлив для замкнутой изолированной системы тел.
Закон сохранения импульса выводится из второго и третьего законов
Ньютона. Покажем это. Для простоты рассмотрим замкнутую систему, состоящую
только из двух тел — шаров с массами  и
и  , которые движутся прямолинейно навстречу друг другу со скоростями
, которые движутся прямолинейно навстречу друг другу со скоростями
 и
и  .
.

Силы тяжести, действующие на каждый из шаров, уравновешиваются силами упругости поверхности, по которой они катятся. Значит, действие этих сил можно не учитывать. Силы сопротивления движению в данном случае малы, поэтому их влияние тоже не будем учитывать. Таким образом, с небольшим приближением можно считать, что шары представляют собой замкнутую систему, т.е. взаимодействуют только друг с другом.

Во время столкновения, длящегося в течение очень короткого
промежутка времени, возникнут силы взаимодействия 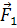 и
и 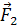 ., приложенные соответственно к первому и второму шару. В
результате действия сил скорости шаров изменятся. Обозначим скорости шаров
после соударения буквами
., приложенные соответственно к первому и второму шару. В
результате действия сил скорости шаров изменятся. Обозначим скорости шаров
после соударения буквами  и
и  ..
..
В соответствии с третьим законом Ньютона силы взаимодействия шаров равны по модулю и направлены в противоположные стороны.

По второму закону Ньютона каждую из этих сил можно заменить произведением массы на ускорение, полученное каждым из шаров при взаимодействии.


Ускорения, как известно, определяются из равенств:


Заменим в предыдущем уравнении ускорения соответствующими выражениями.

Сократим обе части уравнения на Dt

Сгруппируем члены полученного уравнения так, чтобы в левой части уравнения был представлен суммарный импульс шаров до их взаимодействия, а в правой — суммарный импульс после взаимодействия.

Значит, несмотря на то, что импульс каждого из шаров при взаимодействии изменился, векторная сумма их импульсов после взаимодействия осталась такой же, как и до взаимодействия.
Эти уравнения являются математической записью закона сохранения импульса.
А если система тел не замкнута? Можно ли в этом случае пользоваться законом сохранения импульса?
Оказывается можно, но только если:
– Геометрическая сумма внешних сил равна нулю.
– Проекция равнодействующей силы на некоторое направление равна нулю, то вдоль этого направления закон сохранения импульса выполняется.
– И время взаимодействия мало (например взрыв, удар, выстрел).
Обратите внимание: данный закон дает возможность, избегая рассмотрения действия сил, определять скорость и направление движения тел. Этот закон дает возможность говорить о таком важном явлении, как реактивное движение.
Что такое реактивное движение?
На сегодняшний день реактивное движение широко распространено не только среди ракет и самолетов, многие животные тоже используют реактивное движение. Например, такие морские животные, как осьминоги или каракатицы, а также медузы, используют как раз реактивное движение. Они набирают воду, потом ее под давлением из себя выдавливают, и вот это как раз приводит к тому, что они быстро перемещаются под водой.

Под реактивным движением понимают движение тела, возникающее при отделении от тела его части с некоторой относительно тела скоростью.
При этом появляется так называемая реактивная сила, толкающая тело в сторону, противоположную направлению движения отделяющейся от него части тела.
Как вязано реактивное движение с импульсом? Если рассмотреть тело, в котором находится определенное количество газов (а именно за счет газов чаще всего и осуществляется реактивное движение в технике), и если эта масса газов отделяется от тела с большой скоростью, то импульс газов будет равен импульсу самого тела.
Важно понимать, как скорость газов влияет на увеличение скорости оболочки, т.е., чем больше скорость вырывающихся газов, тем больше скорость самой оболочки.


Заметим, что полученная формула записана для мгновенного сгорания газов, а в ракетах не происходит такого — топливо сгорает постепенно.
Реактивное движение бывает двух видов. Реактивное движение «само по себе», характерно для ракет в космосе. Движение ракет обеспечивается наличием топлива и окислителя для него внутри самой ракеты.
Воздушно-реактивное движение — второй вид реактивного движения, характерный для реактивных самолетов. В этом случае никакой окислитель не нужен, потому что самолет летит в воздушном пространстве и, двигаясь с большой скоростью, прокачивает через себя большое количество воздуха (кислорода), который и окисляет топливо, дает большую температуру сгорания. Образуются газы, которые заставляют двигаться самолет вперед.
Чтобы перемещаться в пространстве, необходимо постоянно увеличивать массу горючего. Так, например, чтобы создать такую ракету, которая преодолела бы силу притяжения Солнца, потребуется масса топлива в 55 раз больше, чем масса самой ракеты.
Если говорить об устройстве ракеты, важно понимать, что все ракеты строятся по одному и тому же принципу. Во-первых, это головная часть. Приборныйотсек. Вторая часть — это бак с топливом и окислитель. При смешивании этих двух частей происходит возгорание и сгорание топлива.

Далее идут насосы и обязательно сопло. Форма сопла, того места, откуда вырываются газы, имеет значение. Оказывается, изменение формы позволяет изменять скорость движения.
Большая заслуга в развитии теории реактивного движения принадлежит Константину Эдуардовичу Циолковскому. Он разработал теорию полета тела переменной массы (ракеты) в однородном поле тяготения и рассчитал запасы топлива, необходимые для преодоления силы земного притяжения, основы теории жидкостного реактивного двигателя, а также элементы его конструкции, теорию многоступенчатых ракет, причем предложил два варианта: параллельный (несколько реактивных двигателей работают одновременно) и последовательный, когда реактивные двигатели работают друг за другом.

Труды Циолковского явились теоретической базой для развития современной ракетной техники.
Основные выводы:
– Закон сохранения импульса гласит, что импульс замкнутой системы тел сохраняется при любых взаимодействиях этих тел.
– В случае незамкнутой системы тел закон сохранения импульса используется, если:
– Геометрическая сумма внешних сил равна нулю.
– Время взаимодействия мало (взрыв, удар, выстрел).
– Закон сохранения импульса дает возможность говорить о таком явлении, как реактивное движение. Под реактивным движением понимают движение тела, возникающее при отделении от тела его части с некоторой относительно тела скоростью.
– Большая заслуга в развитии теории реактивного движения принадлежит Константину Эдуардовичу Циолковскому, который предложил теорию многоступенчатых ракет.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 7417
7417

