Задачи на нахождение площади сложных фигур

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

S = a · b

В этой формуле латинской буквой S обозначается площадь, буквами a и b  – стороны прямоугольника.

Выполним задание, в котором надо найти площадь прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в квадратных единицах. В данной задаче это квадратные сантиметры. Также важно помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

3 · 5 = 15 (см²)

Ответ: площадь прямоугольника равна 15 см².

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата равна 16 квадратным сантиметрам.

4 · 4 = 16 (см²)

Ответ: площадь квадрата равна 16 см².

Ну а сейчас перейдём к решению задач, в которых нам надо будет найти площадь сложных фигур.

Найдите площадь фигуры, изображённой на рисунке.

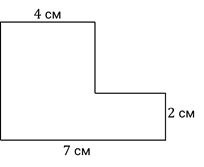
Эта фигура не является ни прямоугольником, ни квадратом. Но мы можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

 А площади прямоугольников мы легко можем найти с помощью известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 = 20 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

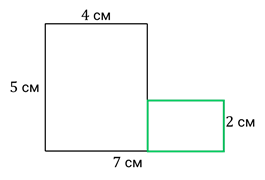
Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6 (см²) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Площадь этой сложной фигуры найти другим способом. Можно разделить её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 = 12 (см²) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 = 14 (см²) – площадь второго прямоугольника

12 + 14 = 26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Решим следующую задачу.

Найдём площадь ещё одной фигуры, изображённой на рисунке.

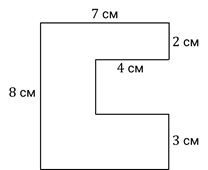
Чтобы найти площадь этой фигуры, тоже разделим её на простые фигуры. Сделаем это вот таким образом.

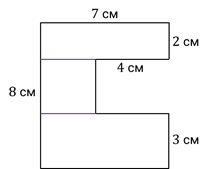
Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 = 14 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3 см.

3 · 3 = 9 (см²) – площадь квадрата

И найдём площадь последнего прямоугольника.

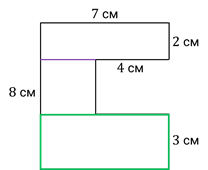
Его ширина равна 3 см. Длина равна 7 см.

3 · 7 = 21 (см²) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму площадей трёх фигур.

14 + 9 + 21 = 44 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см²

Отметим, что площадь этой фигуры можно было бы найти, разделив её на простые фигуры и вот таким образом:

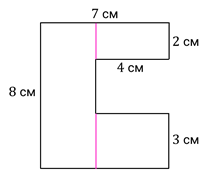
И решим ещё одну задачу.

Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см. Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см и 3 см. Давайте найдём площадь каждого из них.

9 · 5 = 45 (см²) – площадь большего прямоугольника

5 · 3 = 15 (см²) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры найдём, если из площади большего прямоугольника вычтем площадь меньшего прямоугольника.

45 – 15 = 30 (см²) – площадь незаштрихованной фигуры

Ответ: площадь незаштрихованной фигуры равна 30 см².