Друзья, давайте начнём наше занятие с рассмотрения графа.

Напомним, что точки в графе называются вершинами графа. Вершины соединены линиями, которые называются рёбрами графа.
В данном графе по рёбрам можно «пройти» из вершины А в вершину D, то есть существует последовательность рёбер, соединяющих вершины А и D. Такая последовательность называется путём из вершины А в вершину D.
Теперь посмотрите на следующий граф.

В нём есть несколько путей из вершины А в вершину D. Например, есть путь, состоящий из рёбер АC и CD. Его можно обозначить тремя буквами – ACD.
Второй путь подлиннее. Он состоит из рёбер AB, BC и CD. Этот путь можно обозначить четырьмя буквами – ABCD.
Есть более длинный путь из вершины А в вершину D, который состоит из рёбер AB, BF, FE и ED. Его можно обозначить ABFED.
Следующий путь ещё более длинный. Он состоит из рёбер AC, CB, BF, FE и ED. Этот путь можно обозначить ACBFED.
Обратите внимание, что ни в каком из этих путей вершины не повторяются. Такие пути называются простыми путями (или цепями).
А вот путь ABCABCD из вершины А в вершину D заставит нас немного «покружить», ведь нам придётся дважды пройти через вершины А, B и C. Такой путь нельзя назвать простым.
Итак, цепь (простой путь) – это путь в графе из одной вершины в другую, в котором вершины и рёбра не повторяются.
Если граф состоит из одной единственной цепи, то такой граф также называют цепью. Граф без рёбер, состоящий из единственной вершины, тоже считают цепью.
Иногда возникает необходимость выйти из вершины и вернуться в неё же. Такие возвращающиеся в начальную точку пути называют циклами.
Цикл в графе – это замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются.
Также есть такое понятие как простейший цикл. Такой цикл представляет собой петлю, которая состоит из одной вершины и одного ребра.
Отметим, что начальной вершиной цикла можно считать любую вершину. Например, данный граф имеет цикл АBCА. Также этот цикл можно обозначить BCАB, или CABC, или просто ABC.
Если граф состоит из одного единственного цикла, то такой граф также называют циклом. Такой граф состоит из некоторого числа вершин, которые соединены замкнутой цепью.

Теперь посмотрите на два таких графа.

Обратите внимание, что любые 2 вершины первого графа соединены путём. Такой граф называют связным. А вот второй граф называют несвязным, так как в нём есть вершины, которые не соединены путём. Этот граф можно представить как 2 отдельных связных графа.
Запомните, что граф называется связным, если 2 любые вершины в этом графе соединены путём.
Теперь давайте выполним несколько заданий.
Задание первое. Есть ли в графе, изображённом на рисунке, путь из вершины А в вершину C и путь из вершины D в вершину Е? Является ли этот граф связным?

Решение. Чтобы выполнить данное задание, внимательно посмотрим на граф, который изображён на рисунке. Видим, что из вершины А в вершину C есть путь ABC, состоящий из рёбер AB и BC. И есть путь АDC, который состоит из рёбер АD и DC. А вот пути из вершины D в вершину Е нет.
Данный граф является несвязным, так как в нём есть вершины, которые не соединены путём. При этом обратите внимание, что этот граф можно представить как 2 отдельных связных графа.
Задание второе. На рисунке изображён граф. Запишите какие-либо 4 цепи, ведущие из вершины А в вершину D.

Решение. Цепь (или простой путь) – это путь в графе из одной вершины в другую, в котором вершины и рёбра не повторяются.
В данном графе из вершины А в вершину D ведёт цепь, состоящая из рёбер AC и CD. Обозначим её ACD.
Из вершины А в вершину D ведёт цепь, которая состоит из рёбер AF и FD. Обозначим её АFD.
Также из вершины А в вершину D ведёт цепь, состоящая из рёбер AC, CF и FD. Обозначим эту цепь ACFD.
Ещё одна цепь, ведущая из вершины А в вершину D, состоит из рёбер AB, BC, CF, FЕ и ЕD. Эту цепь обозначим АBCFЕD.
Таким образом, мы записали 4 цепи, ведущие из вершины А в вершину D. Очевидно, что есть и другие.
Задание третье. В деревне 9 домов. Соседними считаются участки, у которых есть общий забор. Известно, что у Петра соседи Иван и Антон, Максим сосед Ивану и Сергею, Виктор – Дмитрию и Никите, а также по соседству живут Евгений с Никитой, Иван с Сергеем, Евгений с Дмитрием и Сергей с Антоном. Больше соседей в деревне нет. Может ли Пётр, перелезая через заборы соседних участков, пробраться на участок к Никите?
Решение. Чтобы ответить на вопрос задачи, обозначим дома точками. Соединим непересекающимися линиями те дома, которые являются соседними.

У нас получился несвязный граф, потому что в нём есть вершины, которые не соединены путём.
В задаче спрашивается, может ли Пётр, перелезая через заборы соседних участков, пробраться на участок к Никите. Очевидно, что в получившемся графе нет пути из вершины П в вершину Н, а значит, ответ на этот вопрос: нет.
Ребята, на примере этой задачи мы с вами в очередной раз убедились, что если нарисовать граф подходящим образом, то ответить на вопрос совсем несложно.
На этом мы закончим наше занятие. До встречи на следующих занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход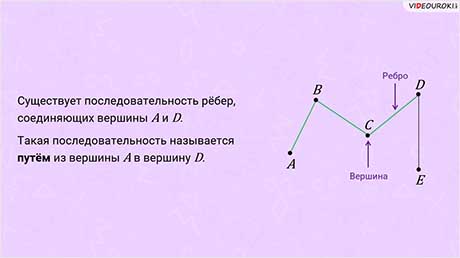




 4454
4454

