Степень вершины графа

Прежде чем приступить к изучению новой темы, напомним, что в математике для изображения и изучения связей между различными объектами применяются графы. При этом отметим, что к аристократам былых времён эти графы не имеют никакого отношения.

Граф – это изображение объектов и связей между ними с помощью точек и линий. Точки в графе называются вершинами графа. Вершины соединены линиями, которые называются рёбрами графа.

Если вершина является концом ребра, то говорят, что ребро исходит из этой вершины или что оно входит в неё.

Важно помнить, что вершина не обязательно должна быть соединена рёбрами с другими вершинами. Вершину, из которой не выходит ни одно ребро, называют изолированной.

Рёбра графа могут пересекаться, но точка пересечения не является вершиной графа.

Теория графов находит применение в различных областях современной математики. Например, при решении логических задач часто бывает непросто запомнить многочисленные условия, данные в задаче, и установить связь между ними. Решать такие задачи помогают графы, дающие возможность наглядно представить отношения между данными задачи.

Давайте решим такую задачу. Одноклассники Андрей, Борис, Вова, Гена, Денис, Лёша и Петя устроили турнир по шахматам. Каждый из участников играет с каждым из остальных один раз. К настоящему моменту Андрей сыграл с Борисом, Геной и Лёшей; Борис, как уже говорилось, с Андреем и ещё с Геной; Вова – с Геной, Денисом и Лёшей. Сколько игр проведено к настоящему моменту?

Решение. Чтобы ответить на вопрос задачи, изобразим участников турнира точками. Если двое участников уже сыграли между собой, то изображающие их точки будем соединять отрезками.

Вот такой граф у нас получился. Заметьте, что точки пересечения рёбер графа не являются вершинами.

У получившегося графа 7 рёбер. Это значит, что к настоящему моменту было проведено 7 игр. Вот таким образом мы ответили на вопрос данной задачи.

Ребята, обратите внимание, что Андрей, Вова и Гена сыграли по 3 партии. Это следует из того, что из соответствующих им вершин исходят по 3 ребра. Борис и Лёша сыграли по 2 партии. Денис сыграл 1 партию. А вот Петя пока не сыграл ни одной партии. В таком случае можно сказать, что степень вершины П равна 0, степень вершины Д равна 1, степени вершин Б и Л равны 2, а степени вершин А, В и Г равны 3.

Как вы уже, наверное, поняли, степень вершины графа – это количество рёбер, исходящих из этой вершины. Иногда степень вершины называют валентностью вершины.

Вершина называется чётной, если из неё выходит чётное число рёбер, и нечётной, если из неё выходит нечётное число рёбер.

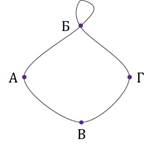
Иногда приходится рассматривать граф с петлёй, то есть с ребром, которое исходит из вершины и входит в неё же, то есть соединяет вершину саму с собой. При подсчёте степени вершины такое ребро считается дважды.

Сейчас перед вами граф с петлёй в вершине Б. Степень вершины Б равна 4.

Теперь давайте вспомним, что если в двух графах вершины связаны рёбрами в одном и том же порядке, то один граф можно получить из другого, передвигая вершины. Такие графы считают одинаковыми.

Чтобы доказать, что два графа одинаковы, нужно показать, что в них поровну вершин и рёбра в одном графе соединяют вершины так же, как и в другом. Если же так сделать не получается, то это не значит, что графы не одинаковые. Возможно, мы просто не сумели найти подходящее соответствие.

Доказать, что два графа не являются одинаковыми, часто можно, подсчитывая степени вершин.

Например, посмотрите на два таких графа.

У каждого из них по 5 вершин и по 4 ребра. Но эти графы не являются одинаковыми, так как у одного из них есть вершина, степень которой равна 3, а у другого такой вершины нет. При этом важно помнить, что если в двух графах поровну вершин и поровну рёбер, то такие графы не обязательно одинаковы.

Теперь сформулируем теорему о сумме степеней вершин. В любом графе сумма степеней всех вершин является чётным числом.

Это действительно так, ведь у каждого ребра 2 конца, а значит, сумма степеней всех вершин в 2 раза больше числа рёбер, то есть чётное число.

Сейчас давайте рассмотрим задачу о рукопожатиях. Во время встречи некоторые участники пожали руки другим. Докажите, что количество участников, сделавших нечётное число рукопожатий, чётно.

Доказательство. Пусть во встрече участвовало n человек, которые сделали чётное число рукопожатий, и k человек, которые сделали нечётное число рукопожатий. Тогда в графе должно быть ровно n вершин чётной степени и k вершин нечётной степени.

Сумма степеней у n вершин чётной степени чётная, так как чётны все слагаемые.

Предположим, что число k нечётное. Тогда сумма степеней этих k вершин также нечётна, поскольку это сумма нечётного числа нечётных слагаемых.

Значит, сумма степеней всех вершин графа будет нечётной, потому что сумма чётного и нечётного чисел – нечётное число. А это невозможно, потому что в любом графе сумма степеней всех вершин является чётным числом. Следовательно, количество участников, сделавших нечётное число рукопожатий, чётно.

Задача о рукопожатиях приводит нас к следующему утверждению. В любом графе количество вершин нечётной степени чётно.

А теперь давайте выполним несколько заданий.

Задание первое. На рисунке изображён граф. Найдите степень вершины Б и степень вершины В.

Решение. Мы знаем, что степень вершины графа – это количество рёбер, исходящих из этой вершины.

Из вершины Б исходят 3 ребра. Значит, степень этой вершины равна 3.

Из вершины В исходят 2 ребра. Следовательно, с её степень равна 2.

Задание второе. На рисунке изображён граф. Сколько у него вершин степени 0, степени 1, степени 2 и степени 3?

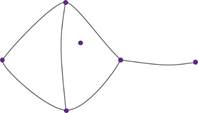
Решение. Чтобы ответить на этот вопрос, внимательно посмотрим на граф, изображённый на рисунке. Видим, что у него есть 1 вершина, из которой не выходит ни одно ребро, то есть она является изолированной, а значит, степень этой вершины равна 0.

Также у графа есть 1 вершина степени 1, 1 вершина степени 2 и 3 вершины степени 3.

Задание третье. Нарисуйте какой-либо граф, в котором 6 вершин со степенями 1, 2, 2, 3, 3, 5.

Решение.

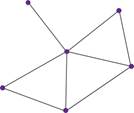
Получился граф, у которого 6 вершин. Из них 1 вершина степени 1, 2 вершины степени 2, 2 вершины степени 3 и 1 вершина степени 5.

Задание четвёртое. Может ли количество вершин нечётной степени в каком-нибудь графе равняться 4, 5, 6?

Решение. Мы знаем, что в любом графе количество вершин нечётной степени чётно.

Следовательно, количество вершин нечётной степени может равняться 4. А вот 5 вершин нечётной степени в графе быть не может. 6 вершин нечётной степени в графе может быть.

Задание пятое. На конференцию собрались 30 учёных. Может ли оказаться так, что 9 из них знакомы ровно с 3 другими, 11 – с 4, а 10 – с 5?

Решение. Представьте, что учёных, которые собрались на конференцию, мы обозначили точками, и соединили линиями тех из них, которые оказались знакомы. Тогда по условию задачи в получившемся графе будет 11 вершин чётной степени. А вот вершин нечётной степени будет 9 + 10, то есть 19.

19 – нечётное число. А мы знаем, что в любом графе количество вершин нечётной степени чётно. Значит, ответ на вопрос данной задачи: нет.

Задание шестое. В некотором графе 6 вершин, степени которых 1, 1, 2, 2, 3, 3 Сколько всего рёбер в этом графе?

Решение. У каждого ребра 2 конца, а значит, сумма степеней всех вершин в 2 раза больше числа рёбер.

Найдём сумму степеней всех вершин графа: 1 + 1 + 2 + 2 + 3 + 3 = 12.

Рёбер в этом графе будет в 2 раза меньше, то есть 6.

Друзья, на этом мы закончим наше занятие. До встречи на следующих занятиях!