Сила упругости. Закон Гука (практика)

Данная тема посвящена решению задач на расчет сил упругости и применение закона Гука.

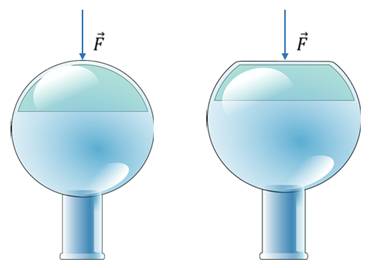
Задача1. Какая колба выдержит большее давление снаружи – круглая или плоскодонная?

РЕШЕНИЕ

И так, очевидно, что при воздействии на дно колбы внешним давлением, колба начнет деформироваться. Деформация — это изменение формы и размеров тела, происходящее из-за неодинакового смещения различных частей одного тела в результате воздействия другого тела.

При этом необходимо вспомнить и тот факт, что тела лучше выдерживают продольные деформации, чем поперечные.

Поэтому, большее давление выдержит круглая колба, так как ее стенки будут испытывать деформацию сжатия, то есть продольную деформацию, а плоское дно — изгиб, то есть поперечную деформацию.

ОТВЕТ: большее давление выдержит круглая колба, так как ее стенки будут испытывать деформацию сжатия, а плоское дно — изгиб.

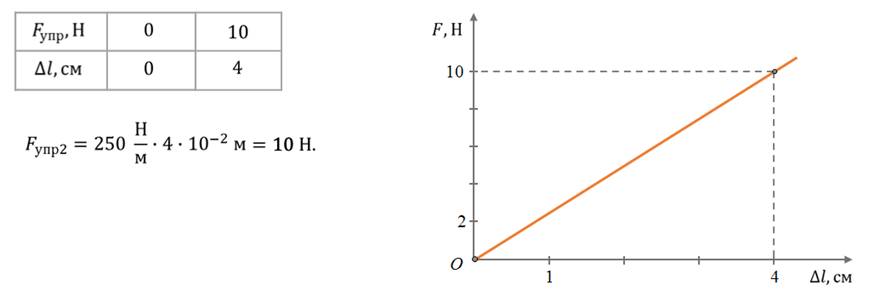
Задача 2. Постройте график зависимости силы упругости, возникающей в деформированной пружине F_упр = f (Δl), от ее удлинения, если жесткость пружины 250 Н/м.

РЕШЕНИЕ

Согласно закону Гука, уравнение зависимости силы упругости, возникающей в деформированной пружине, от ее удлинения имеет вид:

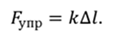
где k — это жесткость пружины. Тогда уравнение примет вид

Как видно, это линейная функция, проходящая через начало координат. Для построения такой прямой достаточно одной точки.

Задача 3. К си­сте­ме из ку­би­ка мас­сой 1 кг и двух пру­жин при­ло­же­на по­сто­ян­ная го­ри­зон­таль­ная сила величиной 25 Н. Система покоится. Между ку­би­ком и опо­рой тре­ния нет. Жест­кость пер­вой пру­жи­ны равна 450 Н/м, вто­рой — 550 Н/м. Определите удлинение пружин.

Задача 4. В лифте находится человек массой 65 кг. Определите вес человека, если лифт движется: а) вниз с ускорением 3 м/с²; б) вверх с ускорением 3 м/с². С каким ускорением должен двигаться лифт, чтобы человек в нем мог ходить по потолку?

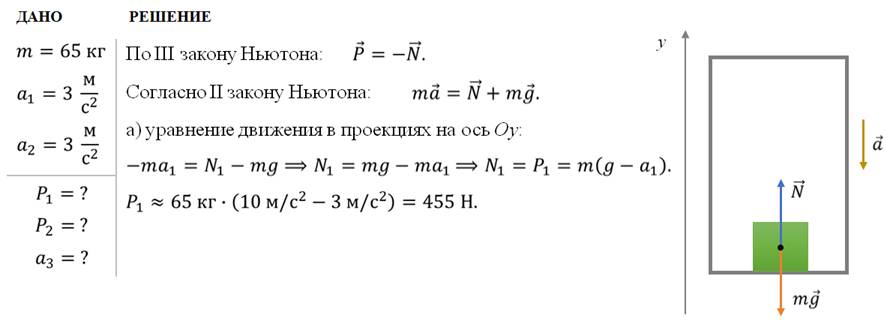
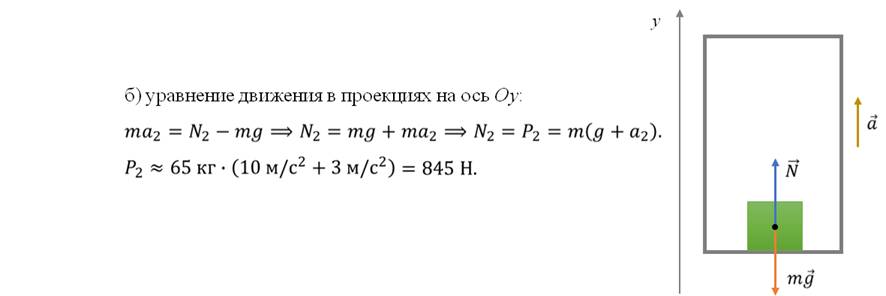
ОТВЕТ: Р₁ = 455 Н; Р₂ = 845 Н; а₃ > g.

Задача 5. На подставке лежит груз массой 1 кг, связанный с прикрепленной к потолку невесомой пружиной. В начальный момент времени пружина не растянута. Подставку начинают опускать с ускорением 0,4g. Через какой промежуток времени груз оторвется от подставки, если жесткость пружины составляет 3 Н/м?

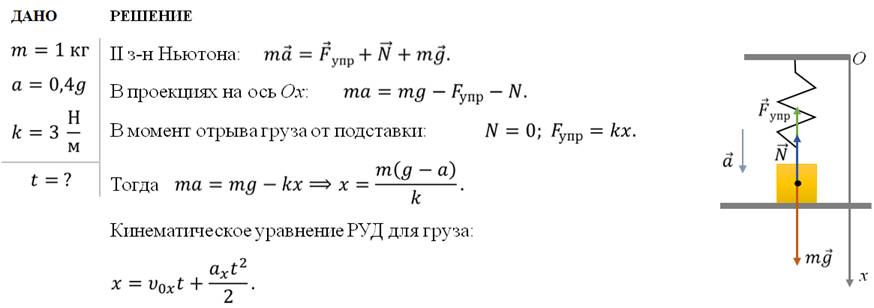
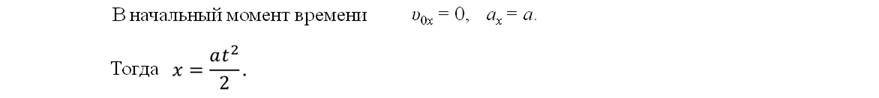
«Истина всегда оказывается проще,

чем можно было предположить»

Ричард Фейнман