Плоское зеркало. Построение изображения в плоском зеркале

Данная тема будет посвящена решению задач на плоское зеркало и построение изображений в плоском зеркале.

Задача 1. Объясните, почему отражения в плоских зеркалах являются симметричными?

Закон отражения света гласит: угол падения равен углу отражения.

Изобразим плоское зеркало и источник света. Исходя из закона отражения света и из того, что зеркало плоское, все падающие на него лучи будут одинаково отражаться. Иными словами, между каждой парой точек в отражении будет сохраняться расстояние. Именно поэтому, наблюдатель будет видеть копию реального объекта (за исключением того, что изображение будет перевёрнуто справа налево).

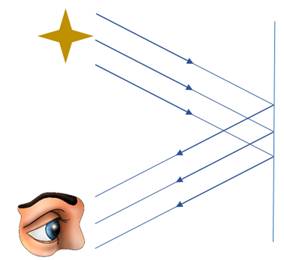
Рассмотреть бытовой пример, когда человек смотрится в зеркало. От каждой точки его тела отражается свет и падает перпендикулярно плоскости зеркала. Исходя из определения падающего луча, угол падения, в этом случае, равен нулю. Значит, равен нулю и угол отражения. Поэтому, все лучи отражаются перпендикулярно поверхности зеркала. В итоге, в зеркале образуется копия человека.

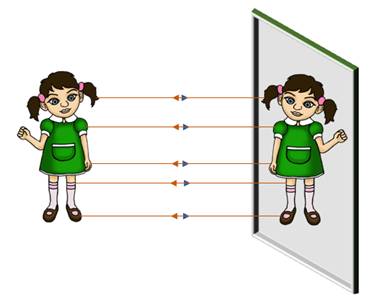
Задача 2. Докажите, что изображение источника света находится на том же расстоянии за зеркалом, на каком сам источник света находится перед зеркалом.

Изобразим на рисунке плоское зеркало и некий источник света.

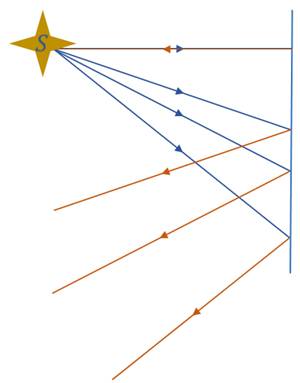
От данного источника света будет падать один луч, направление которого будет перпендикулярно плоскости зеркала. Исходя из определения падающего луча, угол падения, в этом случае, равен нулю. Значит, равен нулю и угол отражения. Поэтому, данный луч отразится перпендикулярно поверхности зеркала. Аналогично, изобразим другие лучи, падающие под разными углами на поверхность зеркала. Также, изобразим отражённые лучи. Изображение источника света за зеркалом будет находиться на пересечении продолжений отражённых лучей.

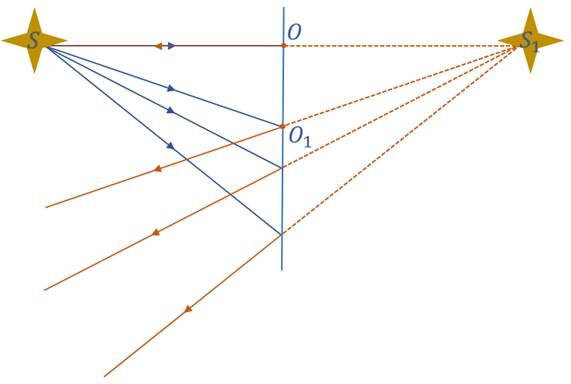
Рассмотрим один из падающих лучей. Восстановим перпендикуляр в точке его падения. Тогда, по закону отражения света, отметим равные углы падения и отражения. Поскольку эти углы равны, и зеркало является плоским, очевидно, что углы между зеркалом и падающим и отражённым лучом также будут равны.

Из рисунка видно, что угол SO₁O равен углу между поверхностью зеркала и отражённым лучом, поскольку эти углы вертикальные.

На чертеже имеются треугольники SOO₁ и S₁OO₁. Эти треугольники равны по второму признаку равенства треугольников.

Во-первых, сторона OO₁ у этих треугольников общая. Во-вторых, углы SOO₁ и S₁OO₁ равны 90º в соответствии с построением. В-третьих, углы SO₁O и S₁O₁O равны. Таким образом, отрезки SO и S₁O имеют одинаковую длину. Поскольку эти отрезки перпендикулярны зеркалу, именно их длина и является расстоянием до источников света.

Задача 3. С помощью карманного плоского зеркала высотой 5 см человек получил на стене «солнечного зайчика». Человек поворачивает зеркало вокруг его центра с линейной скоростью 1 см/с в плоскости, параллельной плоскости стены. Найдите скорость, с которой будет двигаться «солнечный зайчик» по стене, если расстояние между зеркалом и стеной равно 2 м. Считать, что точка падения солнечного луча не смещается. Угол падения равен 30º.

Ответ: 12,4 см/с.

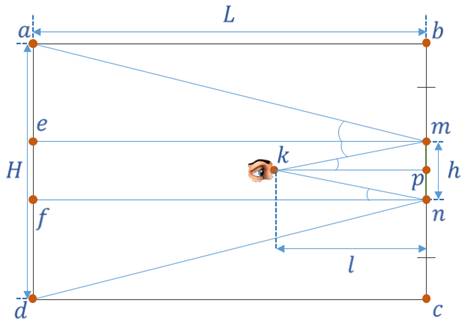
Задача 4. В комнате длиной 3 м и высотой 2,5 м на стене висит зеркало высотой 0,5 м. Найдите минимальное расстояние, на котором должен находиться человек от зеркала, чтобы полностью увидеть противоположную стену. Считать, что зеркало висит на равном расстоянии от пола и потолка.

Ответ: 75 cм.

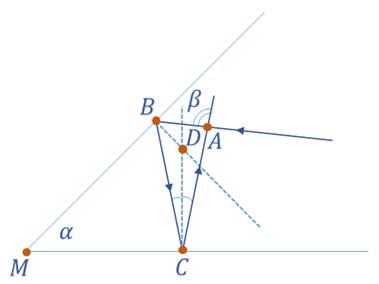
Задача 5. Два плоских зеркала образуют двугранный угол 45º. На одно из зеркал падает луч, расположенный в плоскости, перпендикулярной линии пересечения зеркал. Найдите угол отклонения этого луча от первоначального направления после отражения от обоих зеркал.

Ответ: 90º.