Видеоучебник / Физика / Решение задач по физике. Механика 7-11 класс. / Основные формулы и методические рекомендации по решению задач на законы сохранения в механике

Основные формулы и методические рекомендации по решению задач на законы сохранения в механике

Урок 18. Решение задач по физике. Механика 7-11 класс.

Как известно, любая механическая система может находиться в определенном механическом состоянии. Каждому механическому состоянию системы соответствуют определенный импульс и определенная энергия. На этом уроке мы с вами вспомним определения импульса и энергии, механической работы и мощности. Повторим закон сохранения импульса и закон сохранения и превращения энергии. Вспомним основные определения и формулу, связанные с данным разделом физики, а так же дадим некоторые общие рекомендации по решению задач на законы сохранения в механике.

Конспект урока "Основные формулы и методические рекомендации по решению задач на законы сохранения в механике"

«Лучше знать, даже если знание очень

скоро повлечет за собой гибель, чем

обрести вечную жизнь ценой тусклого

скотского непонимания вселенной, которая

невидимо для нас бурлит во всем своем волшебстве»

Айзек Азимов

В данной теме речь пойдёт о законах сохранения в механике, вспомним некоторые важные формулы, относящиеся к данному разделу, а также дадим несколько советов по решению задач.

Механическая система — это совокупность тел или частей одного и того же тела, взаимодействующих между собой.

Основные вопросы, которые будут затрагиваться при рассмотрении законов сохранения — это импульс и закон сохранения импульса; механическая работа и мощность; а также механическая энергия и закон ее сохранения.

Импульс тела — это векторная физическая величина, равная произведению массы тела на его скорость, а ее направление совпадает с направлением вектора скорости тела. Импульс тела еще очень часто называют количеством движения.

На основании определения импульса тела, можно сформулировать и записать второй закон Ньютона в следующем виде: импульс равнодействующей сил, действующих на данное тело, равен изменению импульса тела.

Из такой записи второго закона Ньютона легко заметить, что импульс тела изменяется под действием данной силы одинаково у тел любой массы, если только время действия сил одинаково.

Импульс системы тел равен геометрической сумме импульсов тел системы. Таким образом, импульс системы тел могут изменить только внешние силы.

При этом для системы тел справедлив закон сохранения импульса, согласно которому в замкнутой системе импульс системы тел сохраняется при любых взаимодействиях этих тел. Система считается замкнутой, если тела системы взаимодействуют только между собой.

Реактивное движение – это движение, возникающее при отделении от тела его части с некоторой относительно тела скоростью.

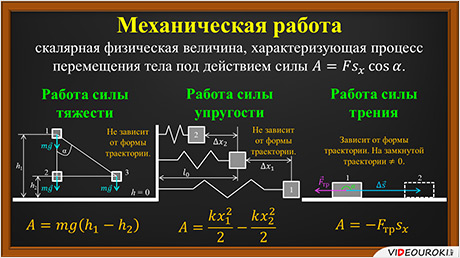
Механической работе – это скалярная физическая величина, характеризующая процесс перемещения тела под действием силы, и численно равная произведению модуля силы на модуль перемещения и на косинус угла между направлением вектора силы и вектора перемещения.

Далее будет рассматривать работу трех сил: силы тяжести, силы упругости и силы трения.

Если тело перемещается под действием силы тяжести из положения 1 в положение 2, определяемые соответственно высотами h₁ и h₂, то работа этой силы будет определяться произведением массы перемещаемого тела на ускорение свободного падения и на разницу высот между начальным и конечным положением тела. При этом следует помнить, что сила тяжести является консервативной силой, поэтому ее работа не зависит от формы траектории, по которой перемещается тело, и на замкнутой траектории равна нулю.

Если движение тела происходит под действием сил упругости, то работа такой силы будет рассчитываться по формуле

где k — это коэффициент жесткости пружины, x₁ и x₂ — ее абсолютное удлинение в положениях один и два соответственно. Так как сила упругости, так же как и сила трения, является консервативной силой, то ее работа тоже не зависит от формы траектории и на замкнутой траектории равна нулю.

При рассмотрении работы силы трения следует учитывать то, что ее вектор направлен противоположно вектору перемещения. Поэтому значение работы будет отрицательным и будет определяться произведением модуля силы трения и модуля перемещения. При этом следует помнить, что, в отличие от силы упругости и силы тяжести, сила трения не является консервативной силой. Поэтому ее работа будет зависеть от формы траектории, по которой перемещается тело, и на замкнутой траектории она отлична от нуля.

Механическая энергия – это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.

Механическую энергию делят на два вида — на кинетическую энергию и потенциальную энергию тела.

Кинетическая энергия — это энергия, которой обладает тело вследствие своего движения. Ее величина зависит от массы тела и его скорости. При этом следует помнить о том, что изменение кинетической энергии тела равно работе равнодействующей всех сил, действующих на тело. Это утверждение называют теоремой о кинетической энергии. Она справедлива независимо от того, какие силы действуют на тело: упругости, трения или тяжести.

Потенциальная энергия — это энергия системы, определяемая взаимным расположением тел (или частей тела друг относительно друга) и характером сил взаимодействия между ними.

Потенциальную энергию разделяют на два вида:

– Потенциальную энергию тела при гравитационном взаимодействии. Потенциальная энергия в поле тяготения определяется как произведение массы тела на ускорение свободного падения и на высоту тела, относительного выбранного нулевого уровня. А ее изменение, взятое с обратным знаком, равно работе силы тяжести.

– Потенциальную энергию упруго деформированного тела. Что касается потенциальной энергии упруго деформированного тела, то это энергия, которая обусловлена взаимодействием частей тела между собой. При этом она равна работе, которую совершает сила упругости, чтобы деформированную пружину вернуть в первоначальное состояние, взятой с обратным знаком. Или говорят, что она равна работе, которую совершают внешние силы, чтобы недеформированную пружину сжать или растянуть.

Следует помнить о том, что тела могут одновременно обладать и кинетической и потенциальной энергией. Поэтому полная механическая энергия тела или системы тел определяется суммой кинетической и потенциальной энергии. Для нее выполняется закон сохранения энергии, согласно которому в замкнутой системе тел, взаимодействующих силами тяготения или силами упругости, полная механическая энергия остается неизменной.

Известно, что для облегчения совершения механической работы издавна используются различные приспособления — простые механизмы. Это устройства, в которых работа совершается только за счет механической энергии. Все простые механизмы служат для преобразования силы.

Наиболее часто встречающимися простыми механизмами являются рычаги и блоки.

Рычаг — это твердое тело, имеющее неподвижную ось вращения, на которое действуют силы, стремящиеся его повернуть вокруг этой оси.

Различают два рода рычага.

К рычагу первого рода относят рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону.

А рычаг второго рода — это рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу.

Блок представляет собой колесо с желобом, укрепленным в обойме. Различают два вида блоков — неподвижный блок и подвижный.

У неподвижного блока ось вращения закреплена и при подъеме грузов она не опускается и не поднимается. Такой блок никакого выигрыша в силе не дает, но позволяет менять ее направление.

В отличие от неподвижного блока, подвижный позволяет получить выигрыш в силе в два раза, а его ось вращения поднимается и опускается вместе с грузом.

Следует упомянуть и об условии равновесия рычага, согласно которому рычаг будет находиться в равновесии, если алгебраическая сумма моментов всех сил, действующих на него, равна нулю. При этом принято считать момент сил, вращающих тело по часовой стрелке, положительным, а против часовой стрелки — отрицательным.

Сведем в таблицу основные формулы законов сохранения энергии.

Формула	Описание формулы
	Импульс тела (количество движения), где m — масса тела, – скорость тела.
	Второй закон Ньютона, где – импульс силы , – время её действия, –изменение импульса тела.
	Закон сохранения импульса, где – импульсы тел до взаимодействия, – импульсы тел после взаимодействия
	Работа постоянной силы, s_x – модуль перемещения, α — угол между вектором силы и вектором перемещения.
	Работа силы тяжести, где h₁ и h₂ — начальная и конечная высота тела относительного нулевого уровня.
	Работа силы упругости, где k — жесткость пружины, х₁ и х₂ — начальное и конечное значение линейной деформации.
	Работа силы трения.
	Мощность, где Δt — промежуток времени, за который совершается работа А, F_υ — проекция силы на направление движения, υ — мгновенная скорость.
	КПД механизма, где Ап – полезная работа, Аз – вся затраченная (совершённая) работа.
	Кинетическая энергия тела.
	Теорема о кинетической энергии, где ∆Е_к — изменение кинетической энергии, А — работа равнодействующей сил.
	Потенциальная энергия тела, поднятого над Землей, где h — высота тела относительно нулевого уровня.
	Потенциальная энергия деформированного тела, где x — линейная деформация.
	Полная механическая энергия системы тел.
	Закон сохранения механической энергии.
	Изменение полной механической энергии системы тел, где A₁ — работа внешних сил, А₂ — работа силы трения.
	Момент силы, где l — плечо силы.
	Условие равновесия рычага.

Методические рекомендации по решению задач на закон сохранения импульса.

1) Внимательно проанализировав условие задачи, сделать чертеж с указанием на нем для каждого тела векторы импульсов в начале и в конце процесса взаимодействия.

2) Установить, является ли рассматриваемая система замкнутой или нет.

3) Если система замкнута или выполняется одно из следующих условий: а) внешние силы уравновешиваются, б) время взаимодействия мало, в) проекция равнодействующих внешних сил на какое-то направление равна нулю, то следует записать закон сохранения импульса в векторном виде.

4) Если же система незамкнута и не выполняется ни одно из прошлых условий, то записать второй закон Ньютона в импульсной форме, рассматривая движение всех тел системы в одной и той же инерциальной системе отсчета.

5) Спроецировать записанные уравнения на выбранные оси координат. Их выбирают так, что бы легко было определить геометрические, а по ним и алгебраические проекции импульсов на соответствующие направления.

6) Если есть необходимость, то следует дополнить систему полученных уравнений кинематическими и динамическими уравнениями движения, ирешить полученную систему относительно искомой величины.

Методические рекомендации по решению задач на закон сохранения и превращения энергии.

1) Делаем чертеж, отметив на нем положения тела, оговоренные в условии задачи (включая начальное).

2) Выбрать нулевой уровень отсчета потенциальной энергии и связываем с ним одну из координатных осей, а другую ось располагаем в плоскости движения тела. Если тело движется под действием силы тяжести, то за нулевой уровень принимаем самое нижнее положение движущегося тела, и записываем формулу для расчета полной механической энергии.

3) Необходимо выяснить, какие силы в рассматриваемой системе являются внешними, внутренними, консервативными и неконсервативными.

5) Для замкнутой системы, в которой действуют только консервативные силы, записываем закон сохранения энергии. Если в замкнутой системе действуют силы трения, то необходимо записать закон сохранения и превращения энергии. А если система незамкнута и внешние силы совершают работу, то надозаписать формулу для определения изменения механической энергии.

6) Составить по необходимости дополнительные уравнения из динамики или кинематики, или дополнить систему законом сохранения импульса.

7) Решить полученную систему уравнений относительно неизвестной величины, проверить размерность и проанализировать полученный результат.