Механические колебания и волны. Звук

Своеобразные движения, которые называются колебательными или просто колебаниями, всем вам хорошо известны. Они широко распространены в окружающем нас мире. Однако при всём разнообразии колебательных движений у всех них есть одна важная особенность: через определённый промежуток времени движение любого из этих тел повторяется.

Давайте вспомним, что процесс, при котором какая-либо физическая величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около некоторого своего среднего значения (положения равновесия) называется механическим колебанием.

На самом деле, если мы отклоним шарик на нити от положения равновесия и отпустим его, то он, пройдя положение равновесия, отклониться от в другую сторону, на мгновение остановится и вернётся в точку начала движения. И если силы сопротивления будут отсутствовать, то такое движение будет повторяться бесконечно долго. Вот такие колебания в физике принято называть свободными колебаниями. Если же в процессе колебаний физические величины, характеризующие колебательное движение, повторяются через равные промежутки времени, то такие колебания называют периодическими.

Для того, чтобы в системе могли возникнуть и существовать свободные колебания, необходимо выполнение ряда условий. Прежде всего, в колебательной системе необходимо наличие положения устойчивого равновесия.

Во-вторых, тело (или материальная точка) должно обладать избыточной механической энергии по сравнению с его энергией в положении устойчивого равновесия.

В-третьих, при выведении тела из положения равновесия в системе должна действовать сила, способная вернуть тело в положение устойчивого равновесия, то есть возвращающая сила.

И наконец, чтобы колебание возникло и продолжалось, избыточная энергия, полученная телом, не должна быть полностью израсходована на преодоление сил сопротивления при возвращении тела в положение равновесия.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел. Так вот, совокупность тел, в которой могут происходить колебательные процессы, мы с вами будем называть механической колебательной системой.

Вы знаете, что для упрощённого рассмотрения тех или иных явлений в науке часто пользуются идеальными моделями. Для колебательных систем такими моделями являются маятники. В общем случае маятником называется твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

Теперь давайте с вами вспомним некоторые важные характеристики колебаний. Итак, первой из них является период колебаний — наименьший промежуток времени, через который полностью повторяется состояние колебательной системы:

Величина, обратная периоду, как и в случае вращательного движения, называется частотой колебаний. Она показывает, какое количество полных колебаний совершается телом в единицу времени:

А наибольшее по модулю отклонение колеблющегося тела от положения устойчивого равновесия — это амплитуда колебаний. Она определяется энергией, которую сообщают точке в начальный момент времени. А единицей её измерения в СИ является метр.

Также важной характеристикой колебательного движения является фаза колебаний — физическая величина, которая показывает, на сколько колебания одного маятника отстают или опережают колебания другого маятника.

Если в любой момент времени скорости одинаковых маятников направлены в противоположные стороны, то говорят, что маятники колеблются в противофазе друг с другом.

Если их скорости в каждый момент времени направлены одинаково, то говорят, что такие маятники колеблются в одинаковых фазах (или синфазно).

А если, например, в момент начала наблюдения скорости обоих маятников направлены в противоположные стороны, а спустя некоторое время их скорости оказываются сонаправленными, то говорят, что колебания маятников происходят с определённой разностью фаз.

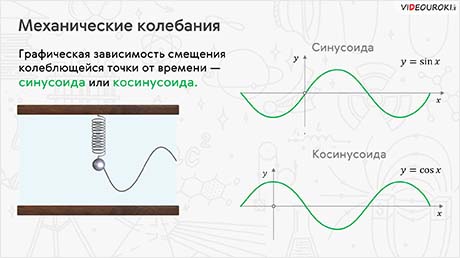
Теперь давайте изучим графическую зависимость смещения колеблющегося тела от времени. Для этого прикрепим к пружинному маятнику грифель от карандаша, а за маятником расположим бумажную ленту и будем равномерно её тянуть. На ленте мы увидим линию, которая по форме будет совпадать с графиком колебаний.

График колебаний нитяного маятника можно получить, проведя аналогичный опыт, используя в качестве груза воронку с песком.

Из результатов опытов видно, что след, который оставляет песок или карандаш на листе бумаги — это кривая, по форме напоминающая синусоиду или косинусоиду. Так вот, периодические изменения во времени физической величины, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.

Если провести ось времени через точки, соответствующие положению равновесия маятника, а перпендикулярно ей — ось смещения, то по графику колебаний можно определить все характеристики колебательного движения. Так, максимальные отклонения маятника от положения равновесия в обе стороны одинаковы по модулю и равны А — это амплитуда колебания. А расстояние между двумя пиками (или двумя впадинами) графика — период колебаний.

Так же с помощью данного графика можно приблизительно определить координату маятника в любой момент времени.

Необходимо отметить, что гармонические колебания полностью подчиняются закону сохранения энергии. И действительно, пусть в положении равновесия потенциальная энергия маятника равна нулю. Сместим тело на некоторое расстояние, тем самым сообщив колебательной системе потенциальную энергию и создав условия для начала колебаний. При движении тела потенциальная энергия системы начинает уменьшаться. Но при этом увеличивается скорость тела, а, значит, и кинетическая энергия системы. В момент прохождения маятником положения равновесия его потенциальная энергия обращается в ноль, а кинетическая энергия достигает своего максимума. После прохождения положения равновесия скорость тела и, следовательно, его кинетическая энергия начинают уменьшаться. Однако, потенциальная энергия системы растёт. Когда смещение тела вновь достигает максимума, то кинетическая энергия становится равной нулю, а потенциальная энергия вновь приобретает максимальное значение. Таким образом, при колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно.

А полная механическая энергия при гармонических колебаниях равна сумме кинетической и потенциальной энергий колебательной системы:

При этом, если в колеблющейся системе отсутствуют силы сопротивления, то её полная механическая энергия остаётся неизменной. Она равна либо потенциальной энергии в момент максимального отклонения от положения равновесия, либо же кинетической энергии в момент, когда тело проходит положение равновесия.

Конечно же реальные колебательные системы практически всегда расположены в какой-либо среде. Поэтому колебательная система может отдавать энергию частицам среды, непосредственно прилегающим к ней, вызывая их вынужденные колебания. Вследствие такого взаимодействия колебательное движение начинает передаваться от одной частицы среды к другой, и колебательный процесс распространяется в среде.

Так вот, процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой, называется механической или упругой волной.

Наиболее отчётливо главные особенности волнового движения можно увидеть, если рассматривать волны на поверхности воды. Например, если мы бросим камень в воду, то в месте его падения по воде пойдут круги — это волны. Если на пути такой волны поместить поплавок, то он начнёт колебаться вверх-вниз, оставаясь при этом практически на месте. Из такого простого наблюдение вытекает одно из важнейших свойств волн: при возбуждении волны происходит процесс распространения колебаний, но не перенос вещества.

Колеблющееся тело, возбуждающее волновое движение частиц среды, называется источником волны или вибратором.

В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают два вида волн: продольные и поперечные.

Поперечной называется волна, если частицы среды совершают колебания в направлении, перпендикулярном к направлению распространения волны. Такие волны могут возникать только в твёрдых телах, так как сдвиг слоёв относительно друг друга в газах и жидкостях не приводит к появлению сил упругости.

Продольной волной называется волна, в которой колебания частиц среды происходят вдоль направления распространения волны. Так как растягиваться и сжиматься может любая среда, то продольные механические волны могут распространяться в любых средах — твёрдых, жидких и газообразных.

Раз волна — это колебание, то волне будут присущи все характеристики, которые соответствуют колебательному движению: амплитуда, период и частота.

Кроме этого возмущение, создаваемое колеблющимся в упругой среде телом, передаётся от одной точки среды к другой не мгновенно, а с определённой скоростью, называемой скоростью волны.

При этом обратим внимание на то, что скорость распространения волны зависит от среды, в которой она распространяется. В основном это связано с тем агрегатным состоянием, в котором находится вещество. Например, в твёрдых телах частицы расположены близко друг к другу и связь между ними велика. Поэтому скорость распространения волны в твёрдых телах будет самой высокой. А, например, в газах скорость волны будет наименьшей, так как взаимодействие между его частицами практически отсутствует.

Также для характеристики волн применяют понятие «длина волны», которое можно ввести двумя способами:

И так, длиной волны называется расстояние, на которое распространяется колебательный процесс в среде за время, равное периоду колебаний её частиц;

Или длина волны — это расстояние между двумя ближайшими точками бегущей волны, которые колеблются в одинаковой фазе.

Если известны период и скорость распространения волны, то, согласно первому варианту определения, длины волны равна произведению её скорости и периода:

Особенно важное место среди всех типов упругих волн занимают звуковые волны (или просто звуки). Под звуком мы с вами будем понимать упругие колебания, распространяющиеся в какой-либо среде и способные вызывать у человека слуховые ощущения.

Из определения следует, что в вакууме звук распространяться не может, что и показал в 1660 году Роберт Бойль.

Также многочисленные опыты и наблюдения показали, что общим для всех тел, издающих звуки, является то, что все они совершают колебательные движения. Но не всякое колеблющееся тело издаёт звуки. Так, например, мы не слышим колебания обычного математического маятника. Всё дело в том, что наше ухо способно воспринимать только акустические звуки, то есть колебания, частота которых находится в пределах 16—20 000 Гц.

Колебания с частотой меньше 16 Гц называют инфразвуком. А колебания с частотой более 20 кГц называют ультразвуком.

Звуковые волны, так же, как и механические, характеризуются скоростью распространения. Именно поэтому во время грозы мы сначала видим вспышку молнии и лишь через некоторое время до нас доносятся раскаты грома.

Если источник звука совершает гармонические колебания, то звук принято называть музыкальным тоном или просто тоном. Хорошее представление о музыкальном тоне даёт звук камертона, который сделан так, что создаёт, практически, звук одной частоты, или один музыкальный тон.

Так как большинство звучащих тел создают целый набор звуковых частот, то для описания создаваемых ими звуков принято использовать целый ряд терминов. Так, например, основным тоном называется звук наименьшей частоты, издаваемый звучащим телом. А обертонами называются звуки более высоких частот, чем основной тон. Их частоты являются кратными частоте основного тона.

Во всяком музыкальном тоне мы можем различить на слух два качества — это громкость и высоту.

Громкость звука зависит от амплитуды колебаний источника звука и особенностей слухового аппарата человека. Единицу громкости звука называют сон (от латинского «сонус» — звук). Но в практических задачах используется внесистемная единица уровня громкости — бел, названная в честь английского изобретателя Александра Белла.

А высота звука — это качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. Она определяется частотой основного тона: чем больше частота основного тона, тем выше звук.

Так как скорость звука зависит от упругих свойств среды и её плотности, то при переходе из одной среды в другую скорость звука скачком изменяется. Поэтому для звуковых волн на границе двух сред могут наблюдаться явления отражения и преломления.

Если отражённая звуковая волна возвратилась к источнику звука, то её называют эхом.

На свойстве звука отражаться от гладких поверхностей основано действие рупора. При его использовании звуковые волны не рассеиваются во все стороны, а образуют узконаправленный пучок, за счёт чего мощность звука увеличивается и он распространяется на большее расстояние.