Статистическая устойчивость и оценка с помощью выборки

Давайте напомним, что выборкой называется набор значений некоторой величины, которые выбраны для изучения всей совокупности. Часто выборку формируют случайным образом и говорят о случайной выборке.

Так как чаще всего невозможно изучить всю совокупность данных (они не всегда доступны или их число неизвестно), то для изучения данных обычно составляют случайную выборку.

Имея выборку из нескольких сотен или тысяч наблюдений, можно с разумной точностью оценить неизвестное среднее, указать, какая доля значений больше или меньше среднего, или найти частоту значений, попадающих в определённый интервал.

Давайте рассмотрим пример, в котором дана выборка значений напряжения в бытовой сети.

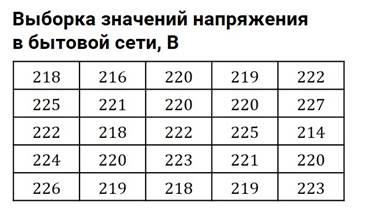
Напомним, что в России номинальное (то есть заявленное) напряжение в бытовых сетях – 220 В. Но в сети напряжение колеблется. Оно редко равно в точности 220 В. Обычно напряжение либо немного выше этого значения, либо немного ниже.

Всего у нас есть 25 значений. Наибольшее значение – 227 В. Наименьшее значение – 214 В.

Давайте сгруппируем данные и построим таблицу частот, выбрав шаг группировки, равный 3 В.

Обратите внимание, что самым «населённым» является четвёртый интервал.

Надо заполнить последний столбец таблицы. Для этого мы будем находить частоты попадания значений в интервал.

Всего дано 25 значений.

В первый интервал не попадает ни одно значение, а значит, частота равна 0.

Во второй интервал попадает 2 значения. Следовательно, частота равна 0,08.

В третий интервал попадает 6 значений. А значит, частота равна 0,24.

В следующий интервал попадает 10 значений. Тогда получается, что частота равна 0,4.

Так как в пятый интервал попадает 5 значений, то частота равна 0,2.

В шестой интервал попадает 2 значения. Следовательно, частота равна 0,08.

В последний интервал не попадает ни одно значение, а значит, частота равна 0.

Запишем сумму найденных значений. Выполним сложение и получим единицу 1.

Так, мы убедились, что частоты найдены верно.

Теперь давайте с помощью этой таблицы найдём, например, как часто напряжение заключено между 217 В и 225 В, то есть найдём суммарную частоту значений в интервалах от 217 В до 225 В.

Найдём среднее выборочное значение. Для этого сумму всех значений разделим на их количество.

Ребята, произведённые расчёты были бы бесполезны, если бы не статистическая устойчивость.

Частоты, средние значения и другие характеристики многих изменчивых величин мало отличаются от таких же характеристик в другой случайной выборке или во всей совокупности данных. Это свойство изменчивых величин называют статистической устойчивостью.

Чтобы статистическая устойчивость проявила себя в нескольких выборках, надо эти выборки сделать в одинаковых условиях. Так как, например, если в одной и той же квартире измерять напряжение в электрической сети первый раз днём, второй раз вечером (когда почти у всех соседей горит свет), а третий раз ночью, то, скорее всего, все три выборки будут значительно отличаться друг от друга.

Чтобы выборка хорошо отражала свойства совокупности данных (а их может быть бесконечно много), лучше всего сформировать её случайным образом. Например, измерения напряжения нужно проводить на протяжении длительного времени в случайные моменты.

Чем больше объём выборки, тем лучше, как правило, проявляет себя статистическая устойчивость.

Статистическая устойчивость даёт возможность оценивать (то есть приближённо находить) частоты и средние значения в бесконечных или плохо доступных массивах данных.

В следующем примере оценим по выборке, сколько времени на протяжении суток напряжение в сети не меньше 220 В.

Для этого воспользуемся таблицей, составленной в предыдущем примере.

Сложим частоты в четырёх последних строках.

В сутках 24 часа. Тогда общая продолжительность периода, когда напряжение не меньше 220 В, приближённо равна 16,32 ч, то есть примерно 16 ч 19 мин.

Следует подчеркнуть, что полученная оценка лишь приблизительно равна истинному значению.

Рассмотрим ещё один пример. На обёртке шоколадного батончика написано, что его масса равна 50 г. Это номинальная (то есть заявленная) масса.

Даны массы 30 купленных таких шоколадных батончиков.

Обратите внимание, что только 2 батончика весят в точности 50 г.

Давайте рассмотрим все такие батончики. Как вы думаете, сколько процентов из них имеют массу более пятидесяти граммов? Ребята, сотни тысяч таких батончиков сейчас лежат в магазинах и кафе в самых разных городах и сёлах. Миллионы таких батончиков давно уже съедены. А ещё миллионы будут выпущены на фабрике. Поэтому очевидно, что взвесить каждый батончик мы не можем. Но мы можем воспользоваться имеющейся выборкой.

В данной выборке 18 батончиков из 30 тяжелее 50 г. Следовательно, в силу статистической устойчивости можно предположить, что доля «тяжёлых» батончиков среди всех приблизительно равна 0,6, то есть 60 %.

Друзья, оценивать доли по выборке можно не только с помощью таблиц, но и с помощью гистограмм.

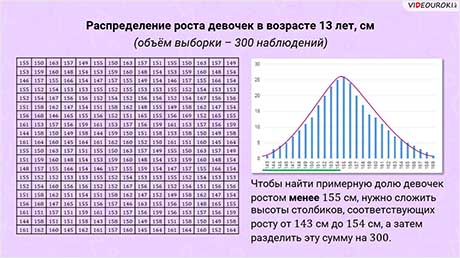
Посмотрите на гистограмму распределения роста девочек в возрасте 13 лет, построенную по случайной выборке объёмом 300 наблюдений.

Например, чтобы найти примерную долю девочек ростом менее 155 см, нужно сложить высоты столбиков, соответствующих росту от 143 см до 154 см, а затем разделить эту сумму на 300.

Но так как гистограммы предназначены для наглядного представления данных, то давайте попробуем «на глаз» оценить долю площади, которую занимают соответствующие столбики. Итак, внимательно посмотрев, заметим, что она чуть меньше половины. Тогда можно предположить, что по выборочным данным доля девочек ростом менее 155 см составляет около 45 %.

В завершение занятия отметим, что в силу случайной изменчивости, оценки, сделанные с помощью выборки, являются приблизительными. Изучением выборочных оценок занимается теория вероятностей. Она часто позволяет дать ответ на вопрос, как сильно могут отличаться истинные частоты и средние от тех частот и средних, которые можно найти по сделанной выборке.

Друзья, до встречи на наших следующих занятиях!