Площадь криволинейной трапеции и интеграл

Сегодня на уроке мы узнаем, что называют криволинейной трапецией. Выясним, как можно вычислить площадь криволинейной трапеции. Узнаем, что называют интегралом от функции  на отрезке .

Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что операцию нахождения первообразной для данной функции называют интегрированием, что в переводе с латинского означает «восстанавливать».

А сейчас рассмотрим фигуру, которая ограничена снизу отрезком  оси . Сверху ограничена графиком непрерывной функции  такой, что  при  и  при . С боков фигура ограничена отрезками прямых  и . Эту фигуру называют криволинейной трапецией.

Отрезок  называют основанием этой криволинейной трапеции.

Выясним, как можно вычислить площадь этой фигуры с помощью первообразной функции .

Итак, пусть  – площадь криволинейной трапеции, основанием которой является отрезок , где  – любая точка отрезка .

При  отрезок  вырождается в точку, поэтому .

При  имеем .  – площадь криволинейной трапеции.

Покажем, что  является первообразной функции , то есть .

Рассмотрим , где .

Отметим, что случай, когда , рассматривается аналогично.

Эта разность равна площади криволинейной трапеции, основанием которой является отрезок .

Справедливо следующее утверждение: найдётся точка  такая, что указанная площадь равна площади прямоугольника с основанием  и высотой , то есть справедливо равенство .

Отметим, что строгое доказательство данного утверждения рассматривается в курсе высшей математики.

Пусть , тогда  и , так как  – непрерывная функция.

,  при . То есть .

Таким образом, мы показали, что  является первообразной функции .

Любая другая первообразная  функции  отличается от  на постоянную, то есть .

При  из этого равенства получаем . Так как , то . Тогда равенство  можно записать так: .

Отсюда  получаем .

Итак, площадь криволинейной трапеции можно вычислить по формуле , где  – любая первообразная функции .

Получается, что вычисление площади криволинейной трапеции сводится к отысканию первообразной  функции , то есть к интегрированию функции .

Разность  называют интегралом от функции  на отрезке  и обозначают . Читается: «Интеграл от А до БЭ ЭФ от икс ДЭ икс», то есть можно записать формулу .

Эту формулу называют формулой Ньютона – Лейбница в честь создателей дифференциального и интегрального исчисления: Исаака Ньютона и Готфрида Вильгельма Лейбница.

Обратите внимание, что правую часть формулы часто записывают вот таким образом: . В таком случае формула примет вид .

Числа  и  называют соответственно нижним и верхним пределами интегрирования. Функцию  называют подынтегральной функцией. Переменную  называют переменной интегрирования.

Далее из двух формул мы получаем, что .

Давайте с вами вычислим площадь криволинейной трапеции, ограниченной графиком функции , осью  и прямыми  и .

Приведённые формулы также справедливы в случаях, когда функция  положительна внутри отрезка , а на одном из концов отрезка или на обоих концах равна нулю.

Найдём площадь криволинейной трапеции, изображённой на рисунке.

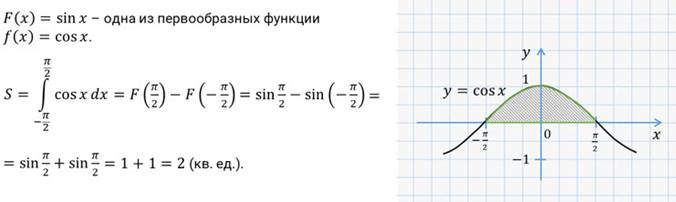
Вообще, исторически интеграл возник в связи с вычислением площадей фигур, которые ограничены кривыми, в частности с вычислением площади криволинейной трапеции. Этому будет посвящено одно из наших следующих занятий.

Давайте рассмотрим рисунок. Здесь изображена криволинейная трапеция, ограниченная прямыми , , осью  и графиком функции . Основание этой криволинейной трапеции – отрезок .

Разобьём его на  отрезков точками , , , …,  . При этом обратите внимание, что эти отрезки не обязательно должны быть равными. Через эти точки проведём вертикальные прямые.

Теперь на каждом отрезке , где , выберем точку  и обозначим .

Тогда площадь прямоугольника с основанием  и  равна .

А вот площадь рассматриваемой криволинейной трапеции приближённо равна сумме площадей построенных прямоугольников:

. Эту сумму называют интегральной суммой функции  на отрезке .

Мы можем увеличивать число точек разбиения отрезка  так, чтобы наибольшая из длин отрезков стремилась к нулю.

В курсе высшей математики доказывается, что для любой непрерывной функции  (не обязательно неотрицательной) на отрезке  интегральные суммы стремятся к некоторому числу, то есть имеют предел, не зависящий от выбора точек . Этот предел называют интегралом (определённым интегралом) от функции  на отрезке  и обозначают .

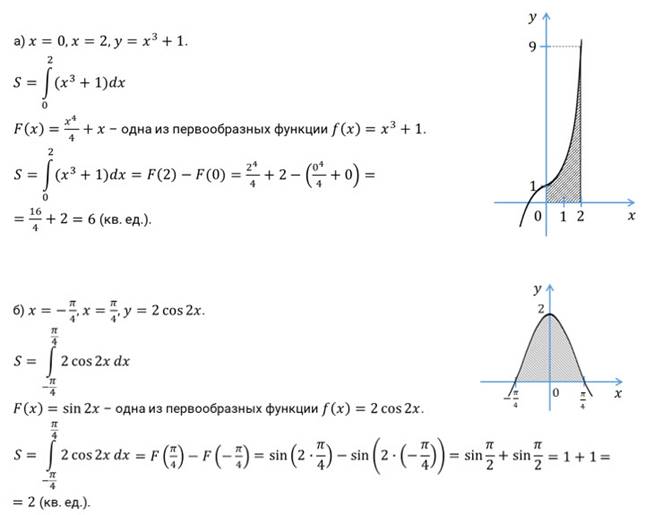
А теперь давайте выполним задание. Найдите площадь криволинейной трапеции, ограниченной прямыми , , осью  и графиком функции :

) , , ; б) , , .

Решение.