Основные формулы и методические рекомендации по решению задач на законы геометрической оптики

В данной теме будут рассмотрены основные формулы и методические рекомендации по решению задач на оптику

Геометрическая оптика изучает законы распространения света в прозрачных средах, отражения света от зеркально-отражающих поверхностей, а также принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств.

Волновая оптика рассматривает волновые свойства света, такие как интерференция, дифракция, поляризационные эффекты и так далее (то есть, те оптические явления, которые выходят за рамки геометрической оптики).

Фотометрия производит количественные измерения характеристик поля излучения, таких как освещённость, световой поток, сила света и так далее. Эта наука является прикладной и используется в различных областях.

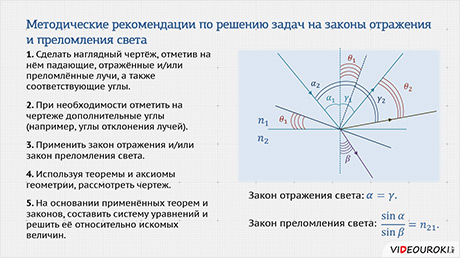
Изобразим на рисунке некоторую среду, на границу которой падает световой луч. Известно, что свет имеет способность преломляться и отражаться. Проведём перпендикуляр в точке падения и обозначим на чертеже необходимые углы.

Угол a называется углом падения. Это угол между падающим лучом и перпендикуляром, восстановленным в точку падения. Угол g называется углом отражения – это угол между отражённым лучом и перпендикуляром, восстановленным в точку падения. Угол b называется углом преломления – это угол между преломлённым лучом и перпендикуляром, восстановленным в точку падения.

Линзой называется любое прозрачное тело, которое с обеих сторон ограничено сферическими поверхностями. Линзы бывают собирающими и рассеивающими. Собирающая (или выпуклая) линза – это линза, края которой тоньше, чем середина. Рассеивающая (или вогнутая) линза – это линза, края которой толще, чем середина.

На чертежах собирающие и рассеивающие линзы обозначаются специальным образом (так, как показано на рисунке).

Тонкая линза – это линза, толщина которой много меньше, чем радиусы кривизны сферических поверхностей, которыми она ограничена.

Проведём линию, проходящую через центры сферических поверхностей, которыми ограничена линза. Эта линия называется главной оптической осью (или просто оптической осью). На этой линии лежит точка, которая называется оптическим центром линзы. Это единственная точка линзы, проходя через которую, свет не преломляется. Если линза симметрична и однородна, то её оптический центр совпадает с геометрическим центром.

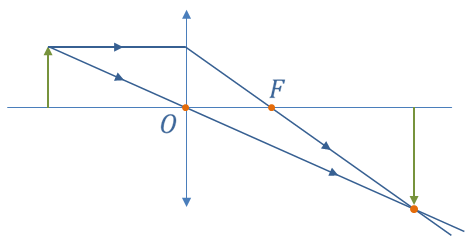
Рассмотрим несколько лучей, направленных на собирающую линзу параллельно оптической оси (чтобы упростить чертёж, мы изобразили всего два луча). После преломления эти лучи пересекутся в некоторой точке F, расположенной на главной оптической оси. Повторим ту же процедуру для рассеивающей линзы: направим на неё два луча параллельно оптической оси. После преломления получаются расходящиеся лучи, которые не пересекутся. Но если начертить продолжения этих лучей, то эти продолжения тоже пересекутся на главной оптической оси (только с другой стороны от линзы).

Полученные точки F называются фокусами линзы. В случае собирательной линзы фокус называется действительным, а в случае рассеивающей линзы – мнимым. Расстояние между оптическим центром линзы и её фокусом называется фокусным расстоянием. Фокусное расстояние зависит от того, насколько сильно преломляются лучи, проходя через данную линзу. Поэтому, вводится такая величина, как оптическая сила – именно этой величиной характеризуется преломляющая способность линзы.

Рассмотрим некоторые понятия и величины, связанные с трёхгранной призмой.

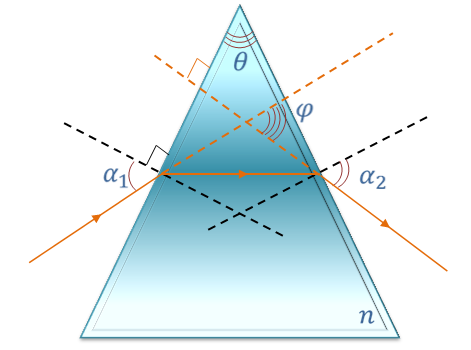
При прохождении через такую призму, луч света отклоняется в сторону основания. Грани, через которые проходит луч света, называются преломляющими гранями призмы. Соответственно угол, образованный этими гранями, называется преломляющим. Угол между падающим лучом и лучом, выходящим из призмы, называется углом отклонения. Именно с углом отклонения связано большинство задач на ход лучей в призме.

Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов интенсивности света.

На рисунке показан простейший способ получения двух интерферирующих волн света.

Полученная картина чередования минимумов и максимумов называется интерференционной картиной. То есть, происходит перераспределение интенсивности света: в одних областях волны суммируются, а в других – погашают друг друга.

Дифракцией света называется совокупность оптических явлений, в результате которых происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.

Если воспользоваться пластиной с круглым отверстием и направить в это отверстие луч света, то в центре светлого пятна получится тёмное пятнышко, и, наоборот, за непрозрачным диском тени будет находиться светлое пятно в центре тени.

На основе явления дифракции был создан прибор, который называется дифракционной решёткой. Он используется для разложения света в спектр и измерения длины волны.

Рассмотрим самое обычное помещение, например, учебный класс. Иногда ученики говорят, что в классе светло или темно. Существует такая величина, как освещённость. Она равна отношению светового потока, падающего на поверхность к площади этой поверхности. Например, когда туча заслоняет солнце, то в классе становится темнее. Имеется ввиду, что освещённость класса уменьшилась, поскольку теперь меньший поток солнечных лучей приходится на ту же площадь. Световым потоком называется отношение полной энергии, выделенной источником света ко времени, в течение которого выделялась энергия.

Сила света – это величина световой энергии, переносимой в определённом направлении в единицу времени.

Рассмотрим некоторые коэффициенты, определяющие оптические свойства различных тел. Коэффициент поглощения – это соотношение поглощенного потока света с падающим потоком. Часть падающего светового потока на стекло поглощается и только часть проходит сквозь него. В противном случае, стекло бы не нагревалось под солнечными лучами. Например, коэффициент поглощения у тел тёмного цвета больше, чем коэффициент поглощения у тел светлого цвета, поэтому, тёмные тела быстрее нагреваются на солнце.

Коэффициент отражения – это соотношение отражённого потока света с падающим потоком. Известно, что часть солнечных лучей отражается от окна.

Коэффициент пропускания – это соотношение пропущенного потока света с падающим потоком. Этот коэффициент связан с двумя предыдущими коэффициентами. Чем больший световой поток тело отражает и поглощает, тем меньший световой поток оно пропускает.

Сведём в таблицу основные формулы геометрической оптики.

Сведём в таблицу основные формулы волновой оптикию

Сведём в таблицу основные формулы фотометрии.

Методические рекомендации по решению задач на законы отражения и преломления света.

1. Сделать наглядный чертёж, отметив на нём падающие, отражённые и/или преломлённые лучи, а также соответствующие углы.

2. При необходимости отметить на чертеже дополнительные углы (например, углы отклонения лучей).

3. Применить закон отражения и/или закон преломления света.

4. Используя теоремы и аксиомы геометрии, рассмотреть чертеж.

5. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.

Методические рекомендации по решению задач на линзы

1. Сделать наглядный чертёж и построить изображение, требуемое для решения задачи.

2. В зависимости от условия задачи, применить формулу тонкой линзы, формулу линейного увеличения линзы или формулу для вычисления оптической силы линзы.

3. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).

4. На основании применённых законов и формул, составить систему уравнений и решить её относительно искомых величин.

Методические рекомендации по решению задач на призмы

1. Сделать наглядный чертёж, построив ход лучей в призме и указав не нём все необходимы углы.

2. Применить формулу для нахождения угла отклонения.

3. При необходимости использовать теоремы и аксиомы геометрии.

4. На основании применённых законов и формул, составить систему уравнений и решить её относительно искомых величин.

Методические рекомендации по решению задач на интерференцию и дифракцию света

1. При необходимости сделать чертёж, соответствующий ситуации, описанной в задаче.

2. Применить условия интерференционных минимумов и максимумов.

3. При необходимости использовать формулу дифракционной решётки.

4. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).

5. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.

Методические рекомендации по решению элементарных задач на фотометрию

1. При необходимости сделать чертёж, соответствующий ситуации, описанной в задаче.

2. Применить формулы освещенности и/или светового потока.

3. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).

4. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.