Получите свидетельство
Вход
И тот взвился под облака;
На миг исчез — и свысока
Шумя, летит на князя снова.
Проворный витязь отлетел
И в снег с размаха рокового
Колдун упал — да там и сел...
А. С. Пушкин (Руслан и Людмила)
Интересным примером прямолинейного равноускоренного движения является свободное падение тела и движение тела, брошенного вертикально. Такие движения тел изучал знаменитый итальянский ученый Галилео Галилей. Он установил, что эти движения равноускоренные.
Измерения показали, что при таких движениях ускорение направлено вертикально вниз и по абсолютному значению равно примерно 9,8 м/с2.
Особенно удивительно и в течение долгого времени было загадкой то, что это ускорение одинаково для всех тел.
При решении задач на свободное падение тел координатную ось естественно направлять по вертикали вверх или вниз, а за тело отсчета выбирать Землю. Координата точки на оси — это ее высота над поверхностью Земли (или глубина под поверхностью Земли).
Формулы для скорости, перемещения и координаты свободно падающего тела и тела, брошенного вертикально, ничем не отличаются от формул для прямолинейного равноускоренного движения.
В этих формулах g — это проекция на ось координат вектора ускорения свободного падения тел; оно положительно и равно + 9,8 м/с2, если координатная ось направлена вниз, и –9,8 м/с2, если ось координат направлена вверх.
Рассмотрим наиболее часто встречающиеся движения тел под действием силы тяжести — свободное падение тел по прямолинейной и криволинейной траектории.
Свободное падение тел по прямолинейной траектории
Задача 1. Тело свободно падает без начальной скорости с высоты h над поверхностью Земли. Определите время движения и скорость тела в последний момент движения.
|
Дано:
|
Решение:
Воспользуемся формулами равноускоренного движения для координаты тела и скорости
Выпишем начальные условия движения.
Тогда уравнение движения примет вид
Из полученного уравнения движения легко определить время полета тела
Скорость в последний момент движения
|
|
|
Задача 2. Мяч бросили вверх с начальной скоростью υ0 направленной вертикально вверх. Определите время всего движения; скорость в последний момент движения; максимальную высоту подъема тела?
|
Дано:
|
Решение:
Воспользуемся формулами для равноускоренного движения тела
Выпишем начальные условия движения.
Уравнения движения
Из этого можно сделать вывод о том, что с какой бы скоростью не бросить мяч с такой же скоростью он вернётся обратно. Определим теперь время подъёма на максимальную высоту
Максимальная высота на которую поднимется мяч
|
|
|
Скорость
движения тела в последний момент движения
Свободное падение тел по криволинейной траектории
Если начальная скорость тела направлена не вертикально, то движение тела будет происходить по криволинейной траектории. Рассмотрим движение тела, брошенного в горизонтальном направлении с некоторой высоты и начальной скоростью.
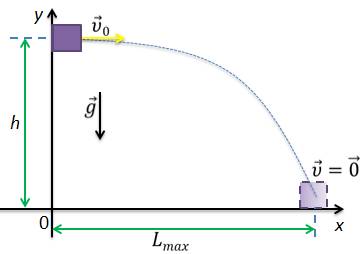
Задача 3. Тело бросили в горизонтальном направлении с начальной скоростью υ0 с высоты h над поверхностью Земли. Определите время движения, дальность полета и скорость тела в последний момент движения.
|
Дано:
|
Решение:
Для решения данной задачи нам понадобится уже не одна, а две оси координат — Ох и Оу, т.к. движение происходит в двух плоскостях. Из рисунка определяем начальные условия движения и проекции величин на координатные оси. Движение по оси Ох
Движение по оси Оу
Проекции на оси координат
Зная высоту, с которой брошено тело, можно определить время всего движения, учитывая, что в этот момент координата игрек равна нулю
За это время тело в горизонтальном направлении пройдет некоторое расстояние, которое называют дальностью полета
Определим скорость в любой момент времени
|
|
|
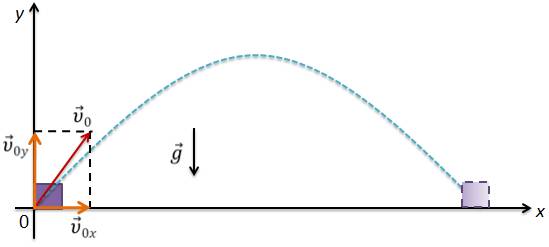
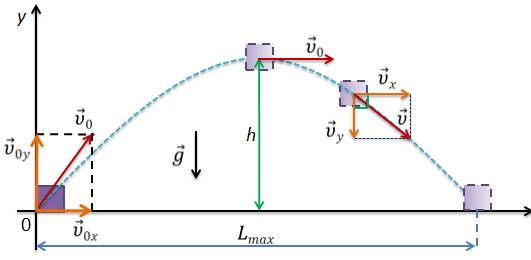
Задача 4. Мяч бросили под углом a к горизонту с некоторой начальной скоростью. Определите: время всего движения; скорость в последний момент движения, максимальную высоту, на которую поднимется тело и дальность полета.
|
Дано:
|
Решение:
Проекции на оси координат
Подставим полученные значения в уравнения движения вдоль каждой из осей Движение по оси Ох
Движение по оси Оу
Из первых двух уравнений вытекает, что проекция скорости на ось икс не зависит от времени, а координата прямо пропорциональна времени, т.е. это кинематические уравнения равномерного движения. Два последних выражения представляют собой кинематические уравнения равноускоренного движения. В верхней точки траетории vy = 0. Тогда
Зная время подъема, можно определить максимальную координату тела по оси Оу или высоту подъема тела
Все время движения определим используя уравнение для координаты тела по оси игрек, которая, в выбранной системе отсчета, в последний момент движения равна нулю.
Полученное квадратное уравнение имеет два корня, первый из которых соответствует начальному моменту времени, а второй — всему времени движения.
В выбранной системе отсчета дальность полета тела — это его конечная координата по оси икс
Мгновенная скорость в любой точке траектории:
|
|
|
Т.о. сложное движение тела, брошенного под углом к горизонту, можно рассмотривать, как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного.
0
13268
