На прошлых уроках мы с вами рассматривали три закона Ньютона — законы движения тел. Согласно им, ускоренное движение тела возможно только под действием силы. Например, падающие тела движутся с ускорением, направленным вниз, так как на них действует сила притяжения к Земле, направленная вниз.

— Но только ли Земля обладает свойством действовать на все тела силой притяжения?
Из седьмого класса вы должны знать, что все без исключения тела притягиваются друг к другу с определённой силой — силой тяготения или гравитационной силой. В этом и заключается явление всемирного тяготения.
Первые попытки объяснения всемирного тяготения появились после установления гелиоцентрической системы мира Коперника. Так, например, английский учёный Ульям Гильберт высказал предположение о том, что наша Земля, как и другие планеты солнечной системы, представляют собой гигантские магниты, поэтому силы, связывающие их, имеют магнитную природу.

Первыми количественными законами, открывшими путь к идее всемирного тяготения, были законы Иоганна Кеплера, опубликованные им с 1608 по1618 годы. И закон инерции Галилея, с которым мы знакомились на одном из прошлых уроков.
После их появления учёные смогли составить механическую задачу на определение движения планет. Первым, кто попытался её решить, был Роберт Гук.

В основе его решения лежало три предположения. Первое заключалось в том, что сила притяжения небесных тел направлена к их центру. При этом будут притягиваться не только части небесного тела, но и другие небесные тела, находящиеся в сфере действия силы.
Второе предположение вытекало из закона инерции Галилея: любое тело, участвующее в прямолинейном движении, будет двигаться по прямой до тех пор, пока не отклонится в своём движении другой действующей силой и не будет вынуждено описывать круг, эллипс или другую сложную траекторию.
И наконец, Гук предположил, что силы притяжения действуют тем больше, чем ближе тело, на которое они действуют, к центру притяжения.
Спустя 10 лет английский астроном Эдмунд Галлей, показал, что сила притяжения убывает пропорционально квадрату расстояния.

Все казалось предугаданным. Но механическая задача не была решена, поскольку учёным не хватало понятия массы и законов динамики, хотя они уже были сформулированы Ньютоном. Невиданная способность выделять в сложности явлений физическую основу и математический гений Ньютона позволили ему решить эту задачу до конца.
Вот как сам Ньютон описывал это открытие: «Я отдыхал в яблоневом саду в имении своих родителей и вдруг увидел в дневном небе Луну. А потом, на моих глазах с ветки дерева упало яблоко. Я уже знал, что яблоко упало не просто так, а под действием гравитационного поля Земли. Знал я и то, что Луна не просто висит на небе, а вращается вокруг Земли. И тут я подумал, а вдруг сила, которая заставляет падать яблоко на землю, и сила, удерживающая Луну от того, чтобы сорваться с орбиты и улететь в космос — это одна и та же сила?»

Окончательно закон всемирного тяготения был опубликован Ньютоном в 1687 году. Он гласит, что любые два тела притягивают друг друга силами, прямо пропорциональными произведению масс этих тел и обратно пропорциональными квадрату расстояния между ними:
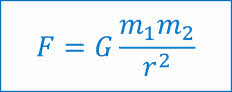
В записанной формуле, G — это коэффициент пропорциональности, одинаковый для всех тел природы. Он носит название гравитационной постоянной, и имеет простой смысл: гравитационная постоянная численно равна силе притяжения двух тел массами 1 кг, находящихся на расстоянии 1 м друг от друга.
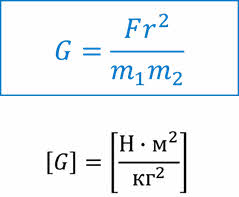
Что касается числового значения G, то оно может быть найдено только из опыта. Первый эксперимент по определению гравитационной постоянной был осуществлён в начале девятнадцатого века Генри Кавендишем. Для измерения гравитационной постоянной Кавендишу пришлось проявить остроумие — придумать чувствительные крутильные весы. Поскольку даже слабые воздушные потоки могли исказить измерения, он разместил свою аппаратуру в ящике, ящик поставил в комнату и наблюдал за движением грузов через оптические зрительные трубы, вставленные в стены комнаты.

Крутильные весы представляли собой двухметровый стержень (коромысло) с двумя небольшими свинцовыми шарами на концах, массы и диаметры которых заранее известны. Стержень подвешивался на тонкой упругой металлической нити. Вблизи малых шаров помещались два больших свинцовых шара также известного диаметра и массы. Сила притяжения между двумя парами шаров заставляла небольшие шары перемешаться к большим. Это вызывало закручивание подвеса. Конечно угол закручивания был чрезвычайно мал, поэтому его определяли с помощью луча света, отражённого от зеркальца. По углу закручивания подвеса можно было определить силу, действующую между большими и малыми шарами.
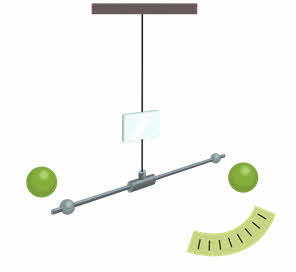
По результатам эксперимента Кавендиш получил значение гравитационной постоянной, отличающейся всего лишь на 1 % от ныне принятого значения.
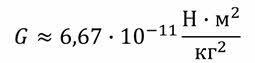
Как видно, гравитационная постоянная — это очень малая величина. Именно поэтому, мы и не замечаем притяжения обычных тел, окружающих нас, и сами не испытываем к ним притяжения. Ведь даже 2 шара массой 1 т каждый, находящиеся в метре друг от друга, притягиваются друг к другу с силой
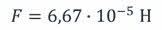
Закрепления материала. Космическая ракета летит на Луну. Расстояние между центрами Луны и Земли равно 60 земным радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке прямой, соединяющей их центры, ракета будет притягиваться Землёй и Луной с одинаковой силой?

В заключении отметим, что закон всемирного тяготения служит надёжной основой для расчёта движения искусственных спутников Земли и межпланетных автоматических станций. Однако надо иметь в виду, что он достаточно точно выполняется лишь для частиц, имеющих малые размеры по сравнению с расстоянием между ними, то есть для материальных точек. Кроме этого, закон всемирного тяготения справедлив для однородных шарообразных тел. А также при взаимодействии сферического тела произвольного размера с телом произвольной формы небольших размеров, находящегося вблизи поверхности сферы.
Для астрономических объектов закон всемирного тяготения выполняется всегда. Однако для тел, сравнительно близких друг к другу (таких, как Земля и Луна), точные измерения обнаруживают отличие силы гравитационного притяжения от той, которая отражена в законе всемирного тяготения. Это связано с неоднородным и несферическим распределением масс.

 Получите свидетельство
Получите свидетельство Вход
Вход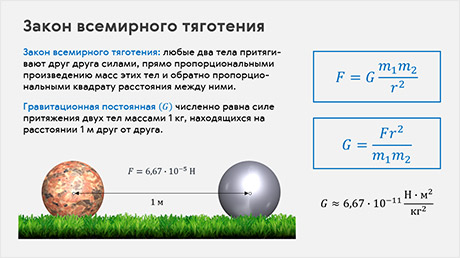



 2
2 9522
9522


Здравствуйте. Благодарим Вас за внимание к нашему проекту. Наши комплекты как методичка, только в современном варианте. Покупать ли их и использовать в работе - выбор каждого клиента. В разделе "Блог" мы предоставляем возможность скачивать многочисленные интересные материалы бесплатно.
Сделайте уроки бесплатными, не покупая комплект