Видеоучебник / Физика / Видеоуроки. Решение задач по физике. Электродинамика. / Взаимодействие токов. Модуль вектора магнитной индукции

Новогодняя распродажа готовых материалов для учителей! Скидки до 50 %

Взаимодействие токов. Модуль вектора магнитной индукции

Урок 15. Видеоуроки. Решение задач по физике. Электродинамика.

Силовой характеристикой магнитного поля, конечно же, является магнитная индукция. Как известно, при протекании электрического тока по проводнику, вокруг него возникает магнитное поле. В данном уроке собраны задачи, предлагающие рассмотреть подобные ситуации.

Плеер: YouTube Вконтакте

Конспект урока "Взаимодействие токов. Модуль вектора магнитной индукции"

«Из всех гипотез выбирайте ту,

которая не пресекает дальнейшего

мышления об исследуемых вещах».

Джеймс Максвелл

Данная тема будет посвящена решению задач на взаимодействие токов и определение модуля вектора магнитной индукции.

Задача 1. По контуру протекает ток, равный 5 А. Этот ток создаёт магнитное поле с индукцией 3 мТл. Найдите радиус контура.

ДАНО:

СИ

РЕШЕНИЕ

Запишем формулу по которой вычисляется магнитное поле кругового тока

Из этой формулы выразим радиус контура

Ответ: 1 см.

Задача 2. Магнитное поле внутри соленоида равно 80 мкТл. Найдите ток, протекающий по виткам соленоида, если на каждый сантиметр соленоида приходится 10 витков.

ДАНО:

СИ

РЕШЕНИЕ

Применим формулу, по которой рассчитывается магнитное поле внутри соленоида

Из этой формулы выразим силу тока

Т.к. все величины входящие в формулу известны, то

Ответ: 157 мА.

Задача 3. К проводнику с сопротивлением 5 Ом приложено напряжение 100 В. Известно, что модуль вектора магнитной индукции поля, создаваемого током в проводнике, равен 2 мТл на расстоянии 2 см от проводника. Найдите магнитную проницаемость среды, в которой находится проводник.

ДАНО:

СИ

РЕШЕНИЕ

Запишем формулу для магнитного поля прямого тока

Закон Ома для участка цепи

Тогда формула для магнитного поля прямого тока с учётом закона Ома будет иметь вид

Из этой формулы выразим магнитную проницаемость среды

Ответ: 10.

Задача 4. По двум параллельным тонким проводникам, находящимся на расстоянии 0,1 м друг от друга, протекают токи 3 А и 2 А в противоположных направлениях. Найдите модуль вектора магнитной индукции в точке, находящейся посередине между проводниками.

ДАНО:

РЕШЕНИЕ

Запишем принцип суперпозиции полей

Магнитное поле прямого тока определяется по формуле

Так как векторы B₁ и B₂ направлены в противоположные стороны, ясно, что модуль результирующего вектора будет равен разности модулей этих векторов

Ответ: 4 мкТл.

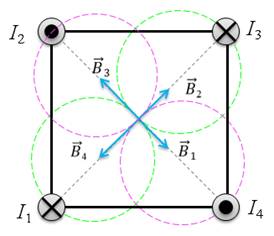
Задача 5. По четырём длинным тонким проводникам, проходящим через вершины квадрата со стороной 5 см перпендикулярно его плоскости, текут токи I₁, I₂ по 15 А и I₃, I₄ – по 20 А. По проводникам, проходящим через противолежащие вершины, текут токи в одном направлении, а по проводникам, проходящим через соседние вершины — в противоположных направлениях. Найдите модуль вектора магнитной индукции в центре квадрата.

ДАНО:

СИ

РЕШЕНИЕ

Чтобы найти модуль вектора магнитной индукции в центре квадрата, необходимо использовать принцип суперпозиции полей

Магнитное поле прямого тока определяется по формуле

Длину диагонали квадрата определим из теоремы Пифагора

Расстояние от центра квадрата до проводника с током будет равно половине длины диагонали

Теперь используем принцип суперпозиции: поскольку векторы B₃ и B₁ направлены в противоположные стороны, можно просто вычислить разность их модулей, чтобы найти магнитное поле в центре квадрата, создаваемое проводниками 1 и 3

Аналогично для проводников 2 и 4: поскольку векторы B₄ и B₂ направлены в противоположные стороны, можно просто вычислить разность их модулей, чтобы найти магнитное поле в центре квадрата, создаваемое проводниками 2 и 4

Исходя из условия, разность между токами I₁ и I₃ равна разности между токами I₂ и I₄. Поэтому, можем заключить, что модули векторов B_1,3 и B_2,4 равны