Получите свидетельство
Вход
Цель:
· уравнения с двумя переменными;
· решения уравнения с двумя переменными;
· степень уравнения с двумя переменными;
· график уравнения с двумя переменными.
Перед вами записаны уравнения:
Все они являются уравнениями с двумя переменными, так как в каждом из них есть две переменные. Возьмём, например, первое уравнение и подставим в него x=3 и y=5:
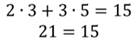
Получили неверное равенство. А если подставим x=3 и y=3, то получим верное числовое равенство.
Определение:
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.
Пара чисел (3; 3) является решением данного уравнения. Но это не единственное решение.
Для определения степени уравнения с двумя переменными, нужно преобразовать его так, чтобы в левой части стоял многочлен стандартного вида, а справа ноль. Тогда степень уравнения считают равной степени данного многочлена.
Чтобы определить степень многочлена с двумя переменными, нужно определить степень каждого одночлена, входящего в состав многочлена, и выбрать из них наибольшую. Степень данного уравнения равна 1.
Пример.
Определить степени уравнений и найти любых два решения.
1. Рассмотрим уравнение:
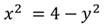
Преобразуем его:
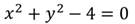
Степень данного уравнения равна 2.
Найдём два любых решения:
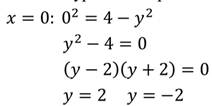
Решением данного уравнения будут пары чисел (0; 2) и (0; -2).
2. Решить уравнение:
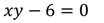
Степень уравнения равна 2.
Найдём два решения уравнения:
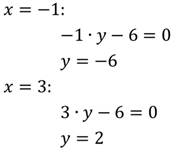
Получили две пары чисел: (-1; -6) и (3; 2).
3. Решить уравнение:
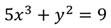
Преобразуем его:
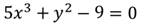
Степень данного уравнения равна 3.
Найдём любые два решения:
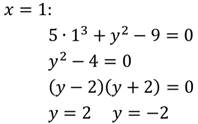
Получили две пары: (1; 2) и (1; -2).
В ходе выполнения заданий стало понятно, что уравнения с двумя переменными имеют много решений. И указать все решения достаточно сложно. Если решением является пара значений, то его можно изобразить на координатной плоскости в виде точки. Так все решения и образуют график уравнения с двумя переменными.
Определение:
Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Пример.
1. Построить график уравнения:
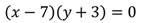
Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
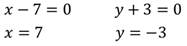
Изобразим график данного уравнения:
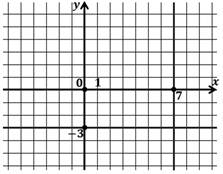
Решением являются две прямые: х=7 и у=-3.
2. Построить график уравнения:
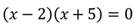
Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
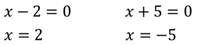
Изобразим график данного уравнения:
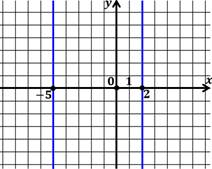
Решением являются две прямые: х=-5 и х=2.
Пример.
Составить уравнения, графиками которых являются пары прямых, изображённых на рисунках.
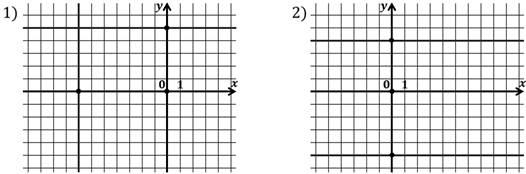
Посмотрим на первый рисунок:
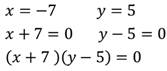
Получили, что прямые являются графиком уравнения.
Обратимся ко второму случаю:
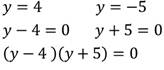
Получили, что эти прямые являются графиком уравнения.
Рассмотрим уравнение:
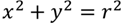
Графиком уравнения является окружность с центром в точке начала координат и радиусом r.
Например, графиком уравнения:
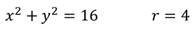
является окружность с r=4.
Пример.
Записать уравнение окружности с центром в точке начала координат и r=6.
Получим уравнение окружности:
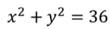
Если центром окружности не является точка начала координат, то уравнение окружности будет выглядеть так:
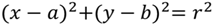
Центр окружности имеет координаты (a; b).
Например,
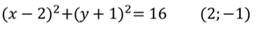
Выполним обратное действие. Но для записи уравнения окружности уже не достаточно только координат центра, необходимо знать и радиус. Например:
0
28143
