Теорема, обратная теореме Пифагора

На предыдущем уроке мы с вами познакомились с теоремой Пифагора, которая звучит следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На этом уроке мы сформулируем и докажем теорему, обратную теореме Пифагора.

Теорема. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный.

Доказательство.

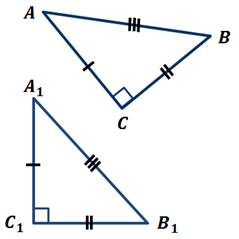
Пусть ABC – треугольник, для которого справедливо равенство: . ,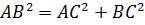

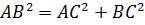Докажем, что 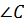 – прямой.

 – прямоугольный.

 – прямой, ,.

,

.

Следовательно, ,то есть,.

 по третьему признаку.

Тогда .

Значит,  – прямоугольный.

Что и требовалось доказать.

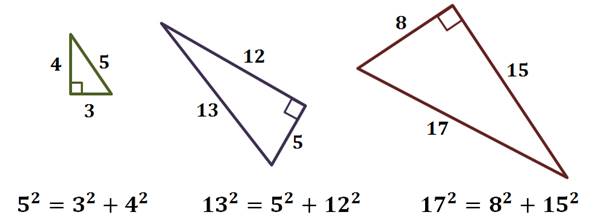
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками. Так каждый из приведённых треугольников является пифагоровым.

В Древнем Египте для построения прямого угла строили прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной три, четыре и пять единиц.

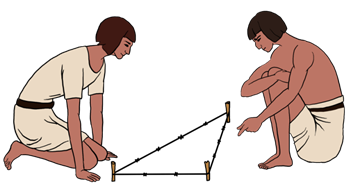
Тогда угол между сторонами, равными трём и четырём, получался прямым.

Задача. Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами: а) , , ; б) , , ; в) , , .

Решение.

Задача. Найдите площадь треугольника, если его стороны равны  см,  см и  см.

Решение.

, тогда  – прямоугольный, .

,

 (см²).

Ответ:  см².

Задача. В равнобедренном треугольнике  длина боковой стороны  равна  см, а основание  –  см. Найдите .

Решение.

 см.

,следовательно,  – прямоугольный, .

Так как  – равнобедренный, то .

,тогда .

Ответ: .

Итак, на этом уроке мы вспомнили теорему Пифагора и познакомились с обратной ей: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный.

Отметили, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.

А также мы поговорили о египетском треугольнике, который представляет собой треугольник со сторонами три, четыре, пять. При этом если пропорционально увеличивать стороны такого треугольника, то полученные треугольники, например, со сторонами шесть, восемь, десять; девять, двенадцать, пятнадцать и так далее также будут прямоугольными.