Получите свидетельство
Вход
Вы уже знакомы с перпендикулярными прямыми на плоскости. Две пересекающиеся прямые называют перпендикулярными, если они образуют 4 прямых угла.
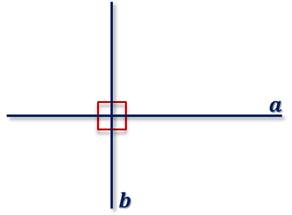
Перпендикулярность
прямых обозначают так 
На этом уроке будем говорить о перпендикулярных прямых в пространстве.
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°.
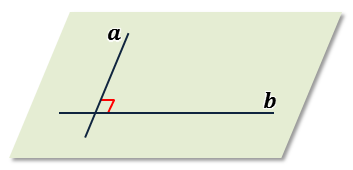
Но так как в 10 классе мы приступили к изучению стереометрии и теперь изучаем свойства фигур в пространстве, то, говоря о перпендикулярных прямых, будем иметь два случая.
Перпендикулярные прямые в пространстве могут быть не только пересекающимися, а ещё и скрещивающимися.
При этом, угол между
скрещивающимися прямыми a и
b будем
изображать так .
В некоторой плоскости выбрав удобную нам точку, проведём через неё прямые a’
и b’ параллельные прямым a
и b соответственно.
Если угол между прямыми a’ и b’ равен 90°, то угол между прямыми a и b так же прямой. А значит, данные прямые перпендикулярны.
Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей,
то и другая прямая перпендикулярна к этой прямой.
Дано:
,
.
Доказать:
.
Доказательство.
1.
,
2.
3.
,
4.
,
5.
Что и требовалось доказать.
Повторим ещё раз. Если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к этой прямой.
Задача.
Назвать все рёбра прямоугольного параллелепипеда 
,
которые
перпендикулярны к ребру 
.
Решение.
Стоит вспомнить, что все грани прямоугольного параллелепипеда являются прямоугольниками.
1.
,
так как 
прямоугольник
2.
,
3.
,
4.
,
так как прямоугольник
5.
,
так как 
прямоугольник
6.
,
7.
,
8.
,
так как прямоугольник
Ответ:
,
,
,
,
,
,
,
.
Обратите внимание.
К точке А на прямой АА1 проведены 2 перпендикуляра, так же как и к точке А1.
В этом и есть главное отличие перпендикуляра к некоторой точке прямой на плоскости от перпендикуляра к точке прямой в пространстве.
Через некоторую точку прямой на плоскости, как вам известно, можно провести только одну перпендикулярную прямую.
А вот в пространстве таких прямых можно провести бесконечное множество. Так как бесконечно много плоскостей проходят через данную прямую и каждая из них содержит ровно один перпендикуляр к данной точке на данной прямой.
Задача.
В тетраэдре 
Доказать,
что 
,
если точки 
и
—
середины рёбер и
соответственно.
Доказательство.
Рассмотрим
.
средняя
линия
,
Что и требовалось доказать.
Подведём итоги нашего урока. Сегодня вы познакомились с определением перпендикулярных прямых в пространстве.
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°.
При этом возможны два случая расположения прямых относительно друг друга: они могут пересекаться и скрещиваться.
Так же мы записали лемму о том, что, если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к этой прямой.
0
7763
