Вопросы занятия:
· вспомнить, что называют квадратным трёхчленом;
· вспомнить, как находят корни квадратного трёхчлена;
· поговорить о разложении квадратного трёхчлена на множители.
Материал урока
Вам хорошо известны такие понятия, как одночлен и многочлен. Среди многочленов выделяют квадратный трёхчлен.
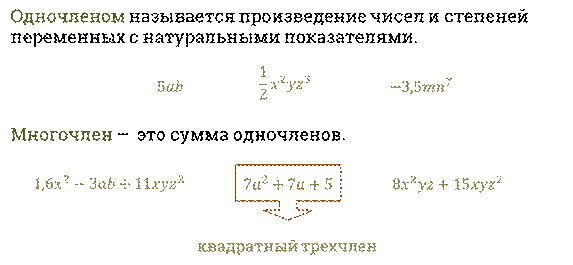
Определение.
Многочлен вида:  ,
где
,
где  ,
,
 и
и
 –
некоторые числа, причём
–
некоторые числа, причём  ,
называется квадратным трёхчленом.
,
называется квадратным трёхчленом.
Числа  ,
,
 и
и
 –
коэффициенты квадратного трехчлена. Причём, число а называют первым
(или старшим) коэффициентом, число
–
коэффициенты квадратного трехчлена. Причём, число а называют первым
(или старшим) коэффициентом, число  –
вторым коэффициентом и число
–
вторым коэффициентом и число  –
свободным членом.
–
свободным членом.
Задание.
Найти среди многочленов те, которые являются квадратными трёхчленами, и назвать их коэффициенты.

Квадратными трёхчленами
будут многочлены:  .
Здесь
.
Здесь  ,
,
 ,
,
 .
.
Многочлен:  .
Здесь коэффициент
.
Здесь коэффициент  ,
,
 ,
,
 .
.
И многочлен:  .
Здесь коэффициент
.
Здесь коэффициент  ,
,
 ,
,
 .
.
Теперь вспомним, как же находят корни квадратного трёхчлена.
Определение.
Вообще, значение переменной, при котором многочлен равен нулю, называют корнем многочлена.
Понятно, что для того
чтобы найти корни квадратного трёхчлена  ,
нужно решить квадратное уравнение
,
нужно решить квадратное уравнение  ,
т.е. найти его корни.
,
т.е. найти его корни.
Задание.
Найти корни квадратных трёхчленов:
 ,
,
 ,
,
 .
.
Решение:
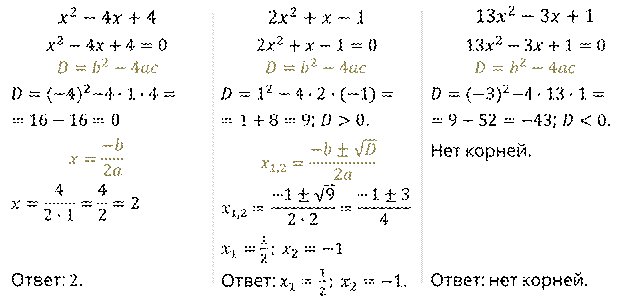
Напомним, что квадратный трёхчлен, как и квадратное уравнение, может иметь: 1 корень, 2 корня или не иметь корней вовсе.
Перейдём к разложению квадратного трёхчлена на множители.
Если дискриминант
квадратного трёхчлена  положителен
положителен
 ,
то трёхчлен можно представить в виде:
,
то трёхчлен можно представить в виде:

где  и
и
 –
корни уравнения
–
корни уравнения  .
.
Если дискриминант
квадратного трёхчлена  равен
нулю
равен
нулю  ,
то трёхчлен можно представить в виде:
,
то трёхчлен можно представить в виде:

где  –
корень уравнения
–
корень уравнения  .
.
Формулы, которые вы видите на экране, называются формулами разложения квадратного трёхчлена на множители.
Если же квадратный трёхчлен
 не
имеет корней, то соответствующий многочлен
не
имеет корней, то соответствующий многочлен  (со
старшим коэффициентом 1) называется неприводимым многочленом второй степени
(так как его невозможно разложить на множители меньшей степени).
(со
старшим коэффициентом 1) называется неприводимым многочленом второй степени
(так как его невозможно разложить на множители меньшей степени).
Задание.
Разложить многочлены на множители:
а)  ;
б)
;
б)  ;
в)
;
в)  .
.
Итак, первый квадратный
трёхчлен:  .
.

Разложим на множители
следующий квадратный трёхчлен:  .
.

И разложим на множители
последний квадратный трёхчлен:  .
.
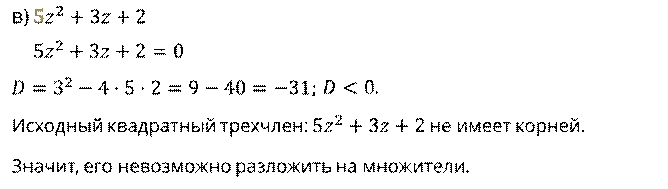
Задание.
Составить квадратный
трёхчлен, корнями которого являются числа 7 и  ,
а старший коэффициент равен 1.
,
а старший коэффициент равен 1.
Итак, запишем квадратный
трёхчлен в общем виде:  .
Если у него есть два корня, то можно разложить его на множители:
.
Если у него есть два корня, то можно разложить его на множители:  .
.
Числа 7 и  корни
трёхчлена по условию.
корни
трёхчлена по условию.
Подставим  и
и
 в
формулу разложения квадратного трёхчлена на множители.
в
формулу разложения квадратного трёхчлена на множители.

Итоги урока
На этом уроке мы рассмотрели тему «квадратный трёхчлен». Вспомнили, что называют квадратным трёхчленом. Как находят корни квадратного трёхчлена. А затем поговорили о разложении квадратного трёхчлена на множители.

 Получите свидетельство
Получите свидетельство Вход
Вход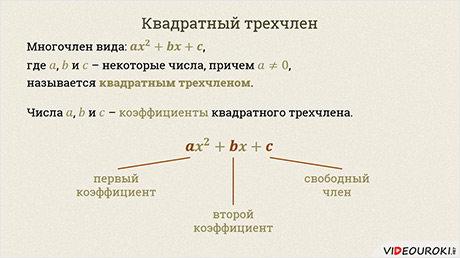



 0
0 4001
4001

