Исследование физических моделей

Вопросы занятия:

·         компьютерное моделирование;

·         процесс построения и исследования модели на примере модели полёта тела, брошенного под углом к горизонту, которая является идеализацией физического процесса.

Физика одна из самых обширных и интересных наук, она является основой естествознания и современного научно - технического прогресса. Одним из наиболее перспективных направлений использования информационных технологий в физическом образовании является компьютерное моделирование физических явлений и процессов.

Мы выяснили, что к основным этапам компьютерного моделирования относятся:

1. Постановка задачи: описание объекта и определение цели моделирования.

2. Построение информационной модели.       

3. Разработка метода и алгоритма реализации компьютерной модели.

4. Разработка компьютерной модели.   

5. Проведение эксперимента.

На сегодняшнем уроке мы попытаемся создать различные модели одного итого же физического процесса. А затем сравним их.

Итак, 1 этап. Постановка задачи: описание объекта и определение цели моделирования.

Камень брошен под углом 45⁰ к горизонту с начальной скоростью 30 метров в секунду.

Необходимо определить:

·        время полёта камня;

·        дальность полёта камня;

·        максимальную высоту подъёма камня;

·        через сколько секунд после начала полёта будет достигнута максимальная высота;

2 этап. Построение информационной модели.

Для решения задачи опишем качественно модель. То есть сформулируем некоторые допущения:

1. Будем считать поверхность Земли плоской, то есть пренебрежём её кривизной.

2. Будем считать, что Земля находится в покое.

3. будем считать, что ускорение свободного падения постоянная величина.

4. Будем считать, что сопротивление воздуха отсутствует.

5. Выберем систему отсчёта и зададим начальные условия, например, пусть начальное время равно нулю, и на поверхности Земли начальная координата (х;у) = (0;0).

3 этап. Разработка метода и алгоритма реализации компьютерной модели.    

Из курса физики известно, что при заданных условиях, движение тела, брошенного с начальной скоростью под углом к горизонту, описывается системой уравнений:

Здесь v₀ – это начальная скорость бросания;

t – время полёта;

α – угол бросания к горизонту.

Также необходимо учесть, что для функций cosα и sinα угол должен быть задан в радианах. Для того чтобы перевести угол в радианную меру нужно

Построим математическую модель, для того чтобы иметь возможность сравнить две модели.

Для начала нарисуем вспомогательный рисунок. Выберем систему координат «XOY». Начало отсчёта совместим с начальным положением камня.

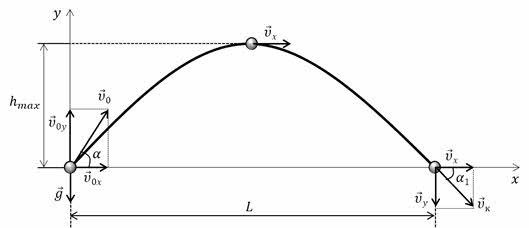
Изобразим траекторию движения и промежуточное положение, которые нам понадобится при решении.

Укажем направление вектора начальной скорости камня, при этом помним, что в случае криволинейного движения, вектор скорости направлен по касательной к траектории. Не забудем указать и направление вектора ускорения свободного падения.

Теперь, в выбранной системе координат, движение камня будем рассматривать как результат наложения прямолинейного равномерного движения вдоль оси «ОХ».

И движение тела, брошенного вертикально вверх, вдоль оси «ОУ».

Сразу укажем на рисунке и направление вектора скорости в промежуточных положениях камня (в верхней точке траектории и в нижней точке траектории).

Теперь давайте выпишем начальные условия движения камня. И так, в выбранной системе координат,

Рассмотрим момент времени, когда камень упал на Землю. В этом случае, его координата по оси «ОУ» будет равна нулю; координата по оси «ОХ» – дальности полёта камня в горизонтальном направлении; а время – времени полёта.

Тогда, с учётом этих условий, запишем уравнения для определения координат камня:

Теперь, зная время полёта камня, можно определить и дальность полёта в горизонтальном направлении. Для этого подставим найденное нами выражение для времени полёта в уравнение для координаты «х». Здесь «L» – это искомая дальность полёта.

Выпишем все полученные результаты.

Конечно же, они оказались завышенными, но это и не удивительно. Ведь мы с вами в начале урока приняли некоторые допущения, а также не учитывали параметры камня.

Итак, мы с вами построили математическую модель полёта тела, брошенного под углом к горизонту и решили задачу по физике.

Теперь построим компьютерную модель, сравним результаты и ответим на поставленный вопрос.

Перейдём к четвёртому этапу. Разработка компьютерной модели

Решим эту задачу с помощью электронных таблиц, например, Microsoft Excel.

Назовём нашу модель: Полёт тела, брошенного под углом к горизонту.

Заполним исходные данные.

Теперь приступим к разработке компьютерной модели. То есть нужно заполнить Расчётную таблицу.

В столбец «Время» введём числа от 0 до 5 секунд с шагом 0,1.

Заполним столбец x(t). В ячейку B 12 вводим формулу: =$A$4*A12*cos $A$6.

Обратите внимание! Ссылки на ячейки с данными для начальной скорости, угла бросания и ускорения свободного падения будут абсолютными.

Скопируем формулу в диапазон ячеек (B13; B62).

Теперь заполним столбец y(t). В ячейку C12 вводим формулу: = $A$4 * А12 * sin $A$6 – (A7*A12^2)/2.

Скопируем формулу в диапазон ячеек (C13; C62).

Проверим адекватность модели. Наша модель создана на основе физических формул.

В выбранной системе отсчёта и начальных условиях модель не соответствует реальному процессу при отрицательных y(t), такие значения из рассмотрения исключаются, то есть если y(t)<0, камень упал и лежит на земле.

Проанализируем значения x(t) и y(t) в таблице и сравним результаты наших моделей.

Мы получили приблизительно одинаковые значения в математической и компьютерной моделях.

Переходим к последнему этапу исследования физической модели. Проведение эксперимента.

Давайте выясним дальность полёта, если камень будет брошен со скоростью 40 метров в секунду.

Для ответа на поставленный вопрос, нам необходимо просто в ячейке A4 изменить значение.

Найдём по расчётной таблице результат. Итак, дальность полёта составит приблизительно 164 метра.

Теперь определим дальность, время полёта и максимальную высоту подъёма, если камень брошен под углом 60⁰ с начальной скоростью 50 метров в секунду.

Обратите внимание. Имея компьютерную модель полёта тема, брошенного под углом к горизонту мы можем сколько угодно раз изменять значения начальных условий и быстро находить результаты. Нам не нужно было снова вспоминать физические формулы, делать подсчёты.

То есть компьютерное моделирование в физике является одним из эффективных методов изучения физических систем. Компьютерные модели зачастую проще и удобнее исследовать, они позволяют проводить вычислительные эксперименты, реальная постановка которых затруднена или может дать непредсказуемый результат.