Резонанс в цепи переменного тока

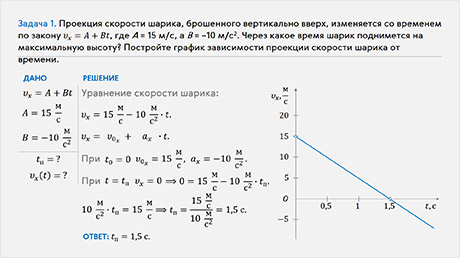
Давайте с вами вспомним, что вывести закон Ома для участка цепи переменного тока, содержащего резистор, катушку индуктивности, конденсатор и источник переменного напряжения нам помогла векторная диаграмма амплитуд напряжений на резисторе, конденсаторе и катушке.

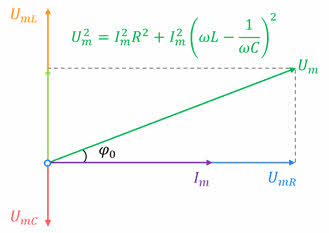
Мы показали, что амплитуда приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол между амплитудами приложенного напряжения и силы тока определяет разность фаз между силой тока и напряжением. Тангенс этого угла, как видно из рисунка, равен отношению разности амплитуд напряжений на катушке и конденсаторе к амплитуде напряжения на активном сопротивлении:

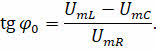
Используя закон Ома для участка цепи нетрудно показать, что этот же угол определяется отношением реактивного сопротивления к активному:

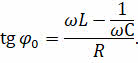
А средняя мощность, выделяемая в цепи на активном сопротивлении, будет определяться выражением, представленном на экране:

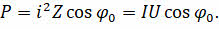
Здесь cos φ₀ — это коэффициент мощности. Являясь безразмерной физической величиной, он характеризует потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей, и показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Из последних двух формул следует, что если реактивное сопротивление цепи равно нулю, то уравнение для мощности примет привычный для нас вид:

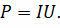
В этом случае в цепи выделяется максимальная мощность — наступает явление резонанса.

Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока или напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура:

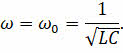
Рассмотрим это явление более подробно. Для начала представим себе, что мы раскачиваем маятник, действуя на него периодически изменяющейся силой. В этом случае маятник будет совершать колебания не самостоятельно, не свободно, а под действием периодической внешней силы. Такие колебания маятника, как мы помним, называются вынужденными колебаниями.

В электрических колебательных контурах также могут происходить вынужденные электромагнитные колебания. Если в каком-либо колебательном контуре, состоящем из катушки индуктивности и конденсатора, всё время действует генератор переменного тока, то ЭДС генератора будет вызывать в этом контуре переменный электрический ток, частота которого будет равна частоте колебаний ЭДС генератора.

Частота этих вынужденных колебаний в общем случае не совпадает с частотой собственных колебании контура:

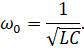
Когда собственная частота колебательного контура далека от частоты ЭДС, действующей в контуре, общее сопротивление контура велико и ток в нём незначителен. Однако если в такой цепи подобрать ёмкость конденсатора и индуктивность катушки так, чтобы их сопротивления оказались равными, то разность фаз между колебаниями силы тока и напряжения станет равным нулю, то есть изменения тока и напряжения будут происходить синфазно:

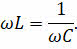
Таким образом, условием возникновения резонанса в колебательном контуре является равенство частоты внешнего подаваемого на контур напряжения частоте собственных колебаний контура:

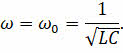
Эту частоту называют резонансной.

При этом условии полное сопротивление контура становится наименьшим и равным активному сопротивлению, а амплитуда силы тока при данном напряжении принимает наибольшее значение. В этом случае амплитуда напряжения на активном сопротивлении равна амплитуде внешнего напряжения, приложенного к участку цепи (U_0r = U₀), а напряжения на катушке индуктивности и конденсаторе одинаковы по модулю и противоположны по фазе:

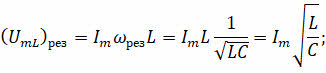
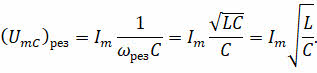
Обратите внимание на то, что амплитудные значения резонансных напряжений на катушке и конденсаторе равны между собой, и они могут значительно превышать амплитуду приложенного напряжения:

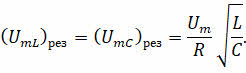
Это явление называется резонансом напряжений. При этом чем меньше активное сопротивление контура, тем сильнее ток в контуре и круче резонансная кривая. Такой случай принято называть острым резонансом.

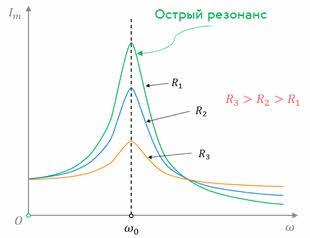
Контур, обладающим острым резонансом, очень чувствителен к колебаниям резонансной частоты. Это широко используется в радио- и электротехнике для усиления колебаний напряжения какой-либо определённой частоты.

Так, например, радиоволны от различных передающих станций возбуждают в антенне радиоприёмника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур, в катушке которого возникают вынужденные колебания силы тока и напряжения. Но только при резонансе из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту обычно осуществляется путём изменения ёмкости конденсатора.

Теперь давайте рассмотрим участок цепи переменного тока, содержащий параллельно включённые конденсатор и катушку индуктивности.

Предположим, что активное сопротивление цепи настолько мало, что им можно пренебречь. Пусть к данной цепи приложено переменное напряжение, изменяющееся по закону синуса:

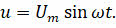
Тогда ток, проходящей в ветви с ёмкостным сопротивлением, будет опережать по фазе приложенное напряжение на π/2. А проходящей в ветви с индуктивным сопротивлением — отставать по фазе на π/2 от приложенного напряжения:

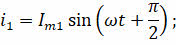
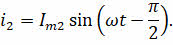
Таким образом, разность фаз токов в двух ветвях равна π, то есть колебания токов в ветвях противоположны по фазе. Амплитуда же тока во внешней цепи равна модулю разности амплитуд сил токов обеих ветвей:

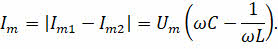
Если частота колебаний в контуре будет равна резонансной частоте, то амплитудные значения сил токов в ветвях будут равны, и амплитуда силы тока во внешней цепи станет равной нулю.

Конечно же, если учесть наличие активного сопротивления, то разность фаз не будет равна π, как и не будет равно нулю амплитудное значение силы тока во внешней цепи. Но оно примет наименьшее возможное значение. При этом амплитуды сил токов в ветвях могут значительно превышать амплитуду тока во внешней цепи.

Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включённые конденсатор и катушку индуктивности, при приближении частоты приложенного напряжения к резонансной частоте называется резонансом токов (или параллельным резонансом).

Это явление используется в резонансных усилителях, позволяющих выделять одно определённое колебание из сигнала сложной формы, а также в индукционных печах, чтобы сила тока в подводящих проводах была гораздо меньше силы тока в катушке.

Для закрепления нового материала давайте решим с вами такую задачу. Контур, состоящий из конденсатора ёмкостью 507 мкФ, катушки индуктивностью 20 мГн и резистора сопротивлением 100 Ом включили последовательно в сеть переменного тока с частотой 50 Гц и напряжением 220 В. Определите силу тока в цепи, сдвиг фаз между напряжением и силой тока, а также резонансную частоту контура.