На этом уроке мы вспомним понятие конуса. Дадим его определение. Рассмотрим, какими элементами он обладает. А также рассмотрим сечения конуса различными плоскостями.
Вокруг нас существует множество объектов, которые являются физическими моделями конуса, или проще говоря, имеют форму конуса.
Например, вафельные рожки для мороженного имеют форму конуса, дорожный конус, пожарное ведро, колпаки для дня рождения, шляпа ведьмочки для хэлоуина тоже имеют форму конуса.

Некоторые архитектурные сооружения.

Декоративным растениям, также придают форму конуса. И многое другое.

Итак, перейдём к самому конусу. Рассмотрим
произвольную плоскость  , окружность
, окружность  с
центром О, лежащую в плоскости
с
центром О, лежащую в плоскости  и прямую
и прямую  ,
перпендикулярную к плоскости
,
перпендикулярную к плоскости  этой окружности.
Через точку
этой окружности.
Через точку  и каждую точку
окружности проведём прямую.
и каждую точку
окружности проведём прямую.

Определение:
Поверхность, образованная этими прямыми, называется конической
поверхностью, а сами прямые – образующими конической поверхности.
Точка  называется вершиной,
а прямая
называется вершиной,
а прямая  называется осью
конической поверхности.
называется осью
конической поверхности.
Определение:
Тело, ограниченное конической поверхностью и кругом с
границей  , называется конусом.
, называется конусом.
Назовём элементы конуса.

Основанием
конуса называется круг, границей которого служит окружность  .
.
Вершиной конуса называется вершина конической поверхности.
Образующими конуса называются отрезки образующих конической поверхности, заключенные между его вершиной и основанием. Отметим, что все образующие конуса равны друг другу.
Боковой поверхностью конуса называется фигура, образованная всеми образующими конуса.
Ось конической поверхности называется осью конуса. А её отрезок (или его длина), заключённый между вершиной и основанием, - высотой конуса.
Конус может быть получен вращением прямоугольного треугольника
вокруг одного из его катетов на  .
.
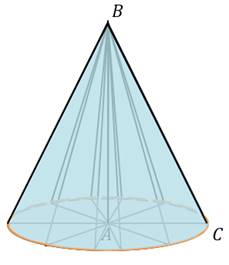
На экране изображён конус, полученный вращением
прямоугольного треугольника  вокруг катета
вокруг катета  .
В этом случае основание конуса образуется вращением катета
.
В этом случае основание конуса образуется вращением катета  ,
а боковая поверхность конуса – вращением гипотенузы
,
а боковая поверхность конуса – вращением гипотенузы  .
.
Рассмотрим сечения конуса различными плоскостями.
Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.
Определение:
Осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось.
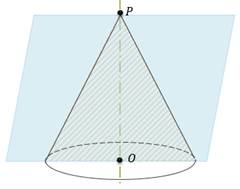
Если секущая плоскость перпендикулярна к оси  конуса,
то сечение конуса представляет собой круг с центром
конуса,
то сечение конуса представляет собой круг с центром  , расположенным на
оси конуса.
, расположенным на
оси конуса.

Замечание. На практике очень часто встречаются предметы, которые имеют иную форму конусов.
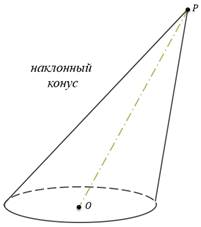
На экране изображён конус, основанием которого является круг, но ось конуса не перпендикулярна к плоскости основания. Такой конус называют ещё наклонным конусом. Однако в дальнейшем мы будем рассматривать только прямые круговые конусы (называя их просто конусы).
Задача: точка
 лежит на высоте
лежит на высоте  конуса,
а точки
конуса,
а точки  и
и  принадлежат
граничной окружности основания конуса. Верно ли, что
принадлежат
граничной окружности основания конуса. Верно ли, что  ?
?
Решение: рассмотрим
треугольники  и
и  .
.

Высота  конуса
перпендикулярна его основанию. А значит, и перпендикулярна любой прямой лежащей
в плоскости основания. Прямые
конуса
перпендикулярна его основанию. А значит, и перпендикулярна любой прямой лежащей
в плоскости основания. Прямые  и лежат в
плоскости основания. Значит, прямая
и лежат в
плоскости основания. Значит, прямая  ,
,  . Отсюда получаем,
что
. Отсюда получаем,
что  и
и  – прямоугольные.
– прямоугольные.
Так как основанием конуса является круги, то  , как радиусы.
, как радиусы.
По условию задачи точка  лежит
на высоте
лежит
на высоте  конуса.
Прямая
конуса.
Прямая  является общей
стороной
является общей
стороной  и
и  . Следовательно,
. Следовательно,  равны по двум
катетам. Отсюда вытекает, что
равны по двум
катетам. Отсюда вытекает, что  .
.
Запишем ответ:  .
.
Задача: длина
образующей конуса равна  см, а высота
конуса –
см, а высота
конуса –  см. Вычислите
радиус основания конуса.
см. Вычислите
радиус основания конуса.
Решение: рассмотрим
 . Напомним, что
высота конуса перпендикулярна основанию конуса, и следовательно,
перпендикулярна его радиусу.
. Напомним, что
высота конуса перпендикулярна основанию конуса, и следовательно,
перпендикулярна его радиусу.

Значит,  – прямоугольный.
– прямоугольный.
По теореме Пифагора найдём его катет  ,
который и является радиусом основания конуса. Получаем, что
,
который и является радиусом основания конуса. Получаем, что  (см).
(см).
Не забудем записать ответ.
Задача: площадь
осевого сечения конуса равна  см2, а
высота конуса –
см2, а
высота конуса –  см. Вычислите
радиус основания конуса.
см. Вычислите
радиус основания конуса.
Решение: рассмотрим
 , который является
осевым сечением конуса.
, который является
осевым сечением конуса.

Напомним, что осевое сечение конуса проходит через ось
конуса и представляет собой равнобедренный треугольник, основание которого –
диаметр основания конуса, а боковые стороны – образующие конуса. Значит,  – равнобедренный.
– равнобедренный.
Площадь треугольника равна  . Отсюда выразим
длину основания треугольника. Получаем, что
. Отсюда выразим
длину основания треугольника. Получаем, что  (см). А так как основание
треугольника есть диаметр основания конуса
(см). А так как основание
треугольника есть диаметр основания конуса  , то можем найти
радиус основания конуса. Напомним, что радиус равен половине диаметра. Значит,
радиус основания конуса равен
, то можем найти
радиус основания конуса. Напомним, что радиус равен половине диаметра. Значит,
радиус основания конуса равен  (см).
(см).
Запишем ответ.
Итоги:
На этом уроке мы вспомнили понятие конуса. Узнали, что
тело, ограниченное конической поверхностью и кругом с границей , называется
конусом. Назвали элементы, из которых состоит конус. А также рассмотрели
сечения конуса различными плоскостями.
, называется
конусом. Назвали элементы, из которых состоит конус. А также рассмотрели
сечения конуса различными плоскостями.

 Получите свидетельство
Получите свидетельство Вход
Вход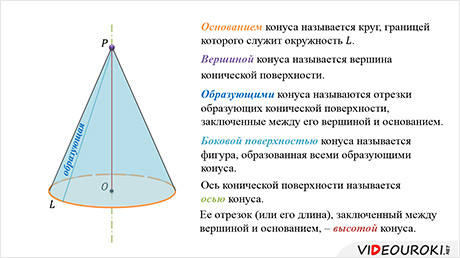



 0
0 5656
5656


