Линейная функция и её график

Вопросы занятия:

·  ввести понятие «линейная функция»;

·  построить графики линейных функций.

Материал урока

Давайте  рассмотрим прямоугольник,

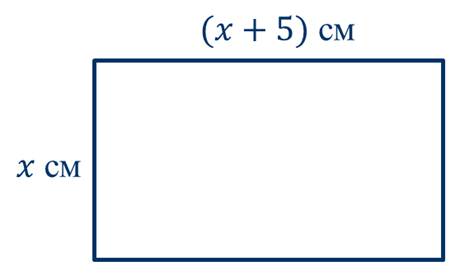
Мы знаем, что периметр прямоугольника равен сумме его длины и ширины, умноженной на 2. А тогда для данного прямоугольника периметр Р можно найти по формуле:

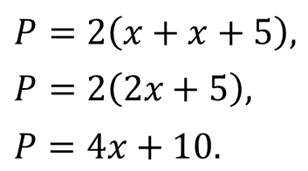
Мы получили формулу, которая выражает зависимость периметра прямоугольника от его ширины.

Обратите внимание, что эта формула имеет вид:

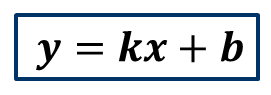
Функции такого вида называют линейными.

В нашем примере x – независимая переменная, k = 4, а b = 10.

Сформулируем определение.

Определение.

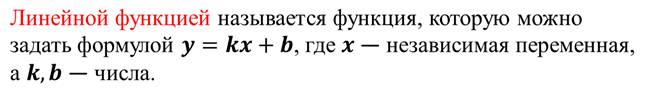
Здесь аргумент х может принимать любое значение.

Линейными, например, являются функции:

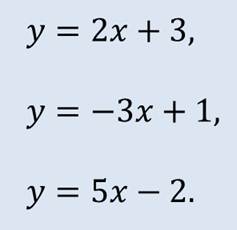
Рассмотренная на предыдущем уроке прямая пропорциональность является частным случаем линейной функции при b = 0.

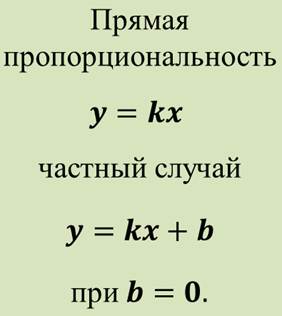
А вот в случае, когда k = 0, линейная функция принимает вид:

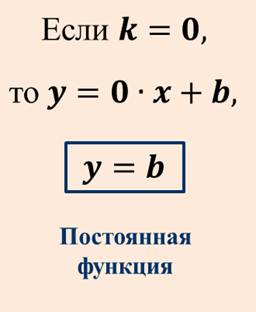
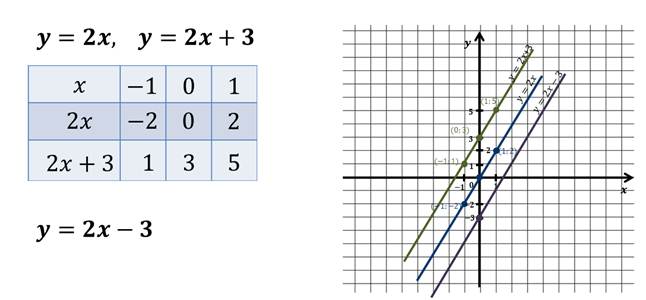
Теперь, давайте рассмотрим:

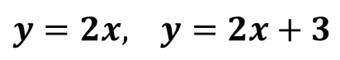
Составим таблицу значений этих функций.

Сейчас мы построим графики этих двух функций.

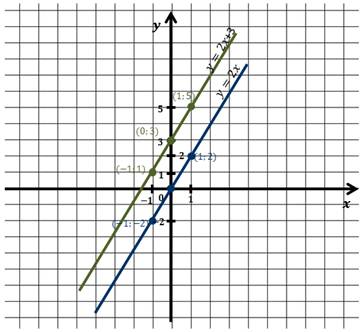
Давайте попробуем сдвинуть график прямой пропорциональности на 3 единицы вверх в направлении оси Oy.

Видим, что прямые совместились.

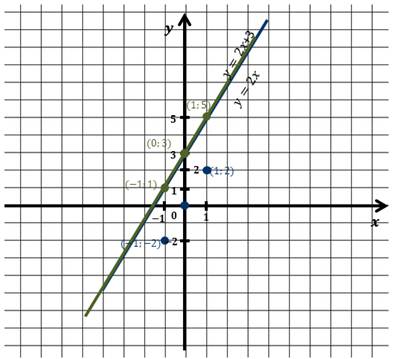
То есть любая точка графика линейной функции получается из соответствующей точки графика прямой пропорциональности, прибавлением к значению функции трёх.

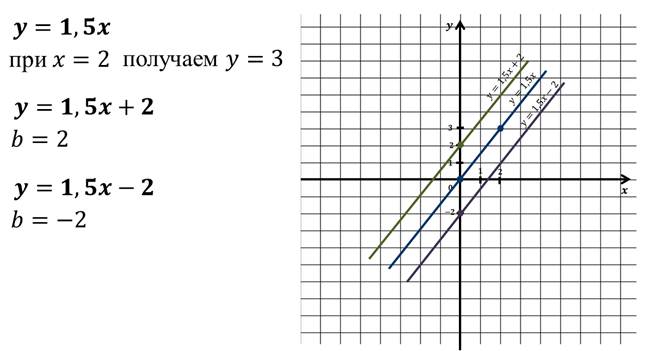
Следовательно, графиком функции y = 2x + 3 является прямая, которая параллельна графику функции y = 2x, проходящая через точку с координатами (0, 3).

Таким же образом можно показать, что графиком функции y = 2x – 3 будет прямая, параллельная прямой y = 2x и проходящая через точку с координатами (0, - 3).

Сформулируем определение.

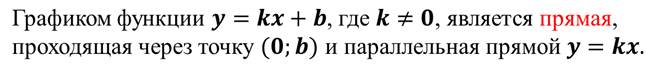
Выполним упражнение.

Пример.

И напоследок рассмотрим график постоянной функции y = b.

Например,