Материал урока.
Прежде чем приступить к изучению нового материала, давайте вспомним, какая фигура называется тетраэдром, вспомним элементы тетраэдра и виды тетраэдра.
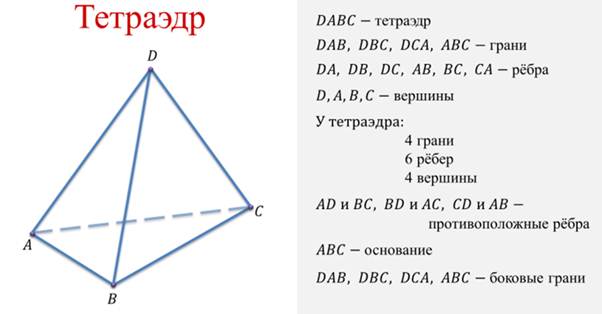
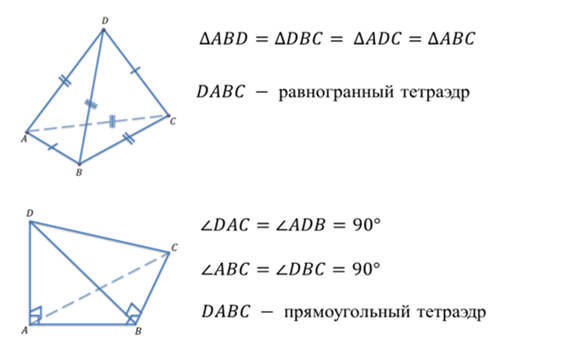
С параллелепипедом мы уже знакомы. Напомним, что в курсе геометрии базовой школы мы определяли параллелепипед как четырехугольную призму, основаниями которой являются параллелограммы.
Сегодня мы дадим немного другое определение параллелограмма.
Рассмотрим два равных параллелограмма ABCD и A1B1C1D1, которые расположены в параллельных плоскостях так, что отрезки AA1, BB1, CC1, DD1 параллельны.
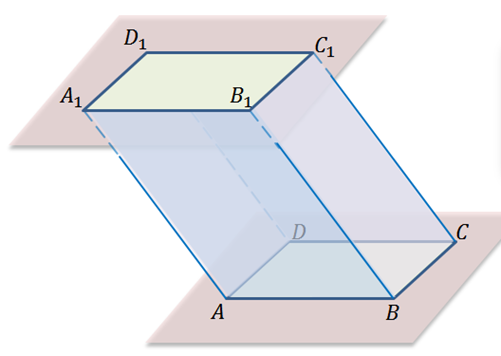
Получили четырехугольники ABB1A1, BCC1B1, CDD1C1, DAA1D1. Рассмотрим один из этих четырехугольников. Например, четырехугольник ABB1A1. Стороны AA1 и BB1 параллельны по условию. По свойству параллельных плоскостей стороны AB и A1B1 параллельны. То есть, четырехугольник ABB1A1 – параллелограмм, аналогично, параллелограммами будут каждый из четырехугольников BCC1B1, CDD1C1, DAA1D1.
Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов ABB1A1, BCC1B1, CDD1C1, DAA1D1называется параллелепипедом и обозначается так: ABCDA1B1C1D1
Параллелограммы, из которых составлен параллелепипед, называются гранями.
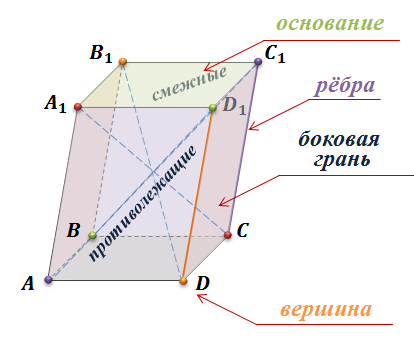
На рисунке изображен параллелепипед ABCDA1B1C1D1. Обратите внимание, все шесть граней параллелепипеда – параллелограммы.
Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра. Например, грани AA1B1B и DD1C1C – противолежащие.
Грани имеющие общее ребро называются смежными. Например, грани AA1D1D и DD1C1C – смежные, ребро DD1 у них общее.
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, - его боковыми ребрами. В нашем случае у параллелепипеда ABCDA1B1C1D1 грани ABCD и A1B1C1D1– его основания. Остальные же грани являются боковыми гранями.
Две вершины, которые не принадлежат одной грани, называются противоположными.
Отрезок, который соединяет противоположные вершины, называется диагональю параллелепипеда. Соответственно у параллелепипеда есть четыре диагонали.
То есть, если в качестве оснований выбрать грани ABCDиA1B1C1D1, то боковыми гранями будут параллелограммы ABB1A1, BCC1B1, CDD1C1, DAA1D1, а боковыми рёбрами будут отрезки AA1, BB1, CC1, DD1.
Мы уже знаем, как изображается параллелепипед. Как и в прочих пространственных фигурах, невидимые рёбра и другие отрезки изображаются штриховыми линиями.
Со свойствами параллелепипеда мы уже знакомы. Повторим их еще раз и докажем с учетом нового определения параллелепипеда.
Первое свойство звучит так: противоположные грани параллелепипеда параллельны и равны. Сразу отметим, что две грани параллелепипеда будут параллельны, если их плоскости параллельны.
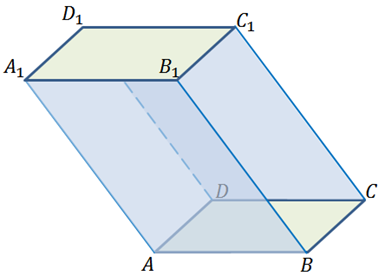
Докажем, например, параллельность и равенство граней ABB1A1 и DCC1D1 параллелепипеда ABCDA1B1C1D1. Поскольку эти грани являются параллелограммами, то можно записать, что AB параллельно DC и AA1 параллельно DD1. То есть две пересекающиеся прямые AB и AA1 одной грани соответственно параллельны двум пересекающимся прямым CD и DD1 другой грани. Значит, по признаку параллельности плоскостей получим, что грани ABB1A1 и DCC1D1 параллельны.
Поскольку все грани параллелепипеда – параллелограммы, то можно записать, что AB равно DC и AA1равно DD1. По этой же причине стороны углов A1AB и D1DC соответственно сонаправлены, и, значит, эти углы равны. Таком, образом мы доказали, что две смежные стороны и угол между ними параллелограмма ABB1A1 соответственно равны двум смежным сторонам и углу между ними параллелограмма DCC1D1, поэтому параллелограммы ABB1A1 и DCC1D1 равны.
Перейдем ко второму свойству. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Доказательство этого утверждения основывается на следующем факте: если две прямые в пространстве параллельны третьей прямой, то они параллельны.
Мы знаем, что диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
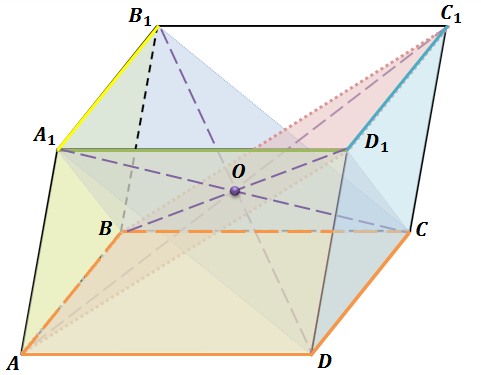
Итак, на экране изображен прямоугольный параллелепипед ABCDA1B1C1D1. Поскольку грани ABCDи AA1D1D – параллелограммы, то BC параллельно AD, BC равно AD, A1D1 параллельно AD, A1D1 равно AD. Из этого следует, что A1D1 параллельно BC и A1D1 равно BC. Поэтому четырехугольник A1D1CB – параллелограмм. А значит, его диагонали A1C и D1B пересекаются в некоторой точке О и делятся этой точкой пополам. Заметим, что эти же диагонали A1C и D1B являются также диагоналями параллелепипеда.
Поскольку грани ABCDиDD1C1C– параллелограммы, то AB параллельно CD, AB равно CD, C1D1 параллельно CD, C1D1 равно CD. Из этого следует, что C1D1 параллельно AB и C1D1 равно AB. Поэтому четырехугольник C1D1AB – параллелограмм. И, следовательно, его диагонали C1A и D1B пересекаются и точкой пересечения делятся пополам. Но серединой диагонали D1B является точка О. Таким образом, диагонали A1C, D1B и C1A параллелепипеда пересекаются в точке О и делятся этой точкой пополам.
Поскольку грани ABCDи AA1B1B – параллелограммы, то CD параллельно AB, CD равно AB, A1B1 параллельно AB, A1B1 равно AB. Из этого следует, что A1B1 равно CD и A1B1 параллельно CD. Поэтому четырехугольник A1B1CD – параллелограмм. И, следовательно, его диагонали A1C и B1D пересекаются и точкой пересечения делятся пополам. Но серединой диагонали A1C является точка О. Таким образом, все четыре диагонали A1C, B1D, C1A и D1B параллелепипеда пересекаются в точке О и делятся этой точкой пополам. Что и требовалось доказать.
Слово параллелепипед происходит от древнегреческих слов паралелос – параллельный, и епипед – плоскость.
Если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым.
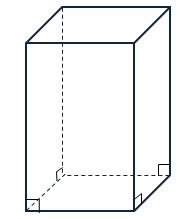
Если параллелепипед не является прямым, то есть если все его боковые ребра не перпендикулярны к плоскостям оснований, то он называется наклонным.
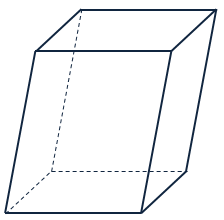
Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
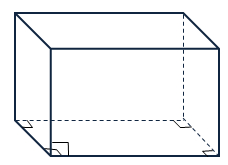
Параллелепипед очень часто встречается в жизни, практически все здания имеют форму параллелепипеда. И многие предметы имеют форму параллелепипеда.
Решим несколько задач.
Задача. Дан
параллелепипед 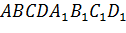 . Доказать, что
диагональ
. Доказать, что
диагональ 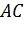 параллельна
параллельна 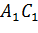 .
.
Доказательство.
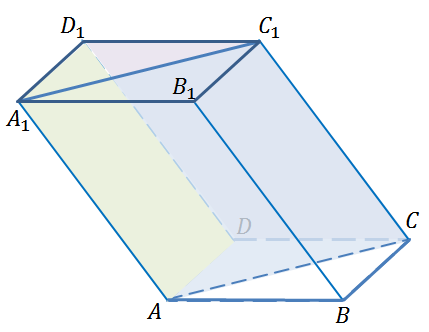
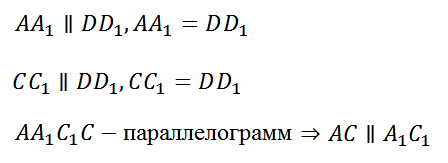
Что и требовалось доказать.
Задача. Сумма
всех рёбер параллелепипеда 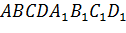 равна
равна 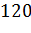 cм.
Найдите каждое ребро параллелепипеда, если
cм.
Найдите каждое ребро параллелепипеда, если 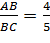 ,
а
,
а 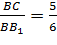 .
.
Решение.
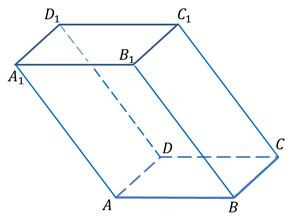
Из соотношений выразим длины ребер AB и BB1 через длину ребра BC.
Получим, что ABравно 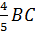 , BB1 равно
, BB1 равно 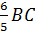 .
.
У параллелепипеда двенадцать ребер, из них четыре ребра равны ребру AB, четыре ребра равны ребру BB1, четыре ребра равны ребру BC. Заменим ребра AB и BB1 и их выражением через ребро BC, получим, что 12BC=120. Тогда получим, что длина ребра BC= 10. Подставим это значение в формулу для нахождения длин ребер AB и BB1, получим, что AB= 8, а BB1= 12.
Кратко запишем решение задачи.
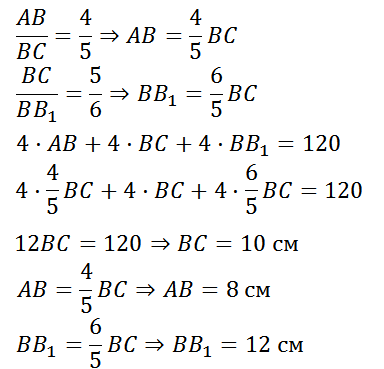
Подведем итоги урока. Сегодня на уроке мы познакомились с еще одним пространственнымтелом – параллелепипедом. Познакомились с элементами параллелепипеда, решили несколько задач по данной теме.

 Получите свидетельство
Получите свидетельство Вход
Вход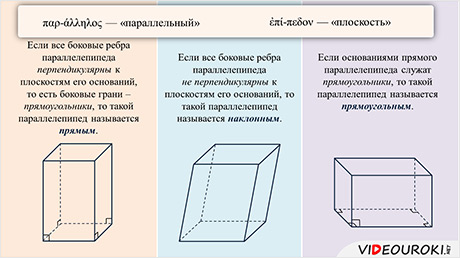



 0
0 7503
7503

