Среди окружающих нас предметов много таких, которые мы называем круглыми. Например, кольцо, гимнастический круг, часы, торт, дорожный знак…
Но кольцо, гимнастический круг имеют форму окружности, а часы, торт и дорожный знак – форму круга.
В начальных классах вы уже знакомились с такими фигурами, как окружность и круг.

Давайте начертим окружность с помощью циркуля. Для этого надо установить остриё циркуля (иглу) на бумагу, а вторую ножку циркуля, которая с карандашом, будем вращать вокруг первой. Карандаш начертит линию, которая и называется окружностью.

Окружность – это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.
Точка, в которой мы установили остриё циркуля, является центром окружности.
На рисунке центр окружности обозначен точкой О.
Отметим на окружности некоторую точку А и соединим центр окружности с точкой А. Получим отрезок ОА, который называют радиусом.
Отрезок,
соединяющий центр окружности с любой точкой, лежащей на окружности, называют радиусом.
Латинское слово «радиус» в переводе на русский язык означает «спица в колесе».
Радиус принято обозначать маленькой латинской буквой  .
.
Теперь давайте отметим на окружности любые две точки, например, B и C. Соединим их отрезком. Полученный отрезок BC является хордой окружности.
Хорда окружности – это отрезок, соединяющий любые две точки окружности. Хорда – это греческое слово, которое в переводе на русский язык означает «струна».
Отметим на окружности точки Е и F и соединим их отрезком.
Этот отрезок является хордой. Но у этой хорды есть своё название.
Хорду, проходящую через центр окружности, называют диаметром. В переводе
с греческого «диаметр» означает «поперечник». Диаметр обозначают маленькой
латинской буквой  .
.
Диаметр окружности равен двум её радиусам. То есть диаметр в 2
раза больше радиуса, то есть верно равенство  .
.

В окружности можно провести бесконечно много радиусов и диаметров. Причём все радиусы одной окружности равны между собой. Все диаметры одной окружности тоже равны между собой.
Отметим на окружности две точки, например, М и N. Эти точки делят окружность на две части, каждую из которых называют дугой окружности. Точки М и N называют концами дуг.

Древние греки считали окружность самой совершенной фигурой. Совершенство окружности заключается в расположении всех её точек на одинаковом расстоянии от центра. Окружность – это единственная фигура, которая может «скользить сама по себе», вращаясь вокруг центра.
Именно поэтому колёса делают круглыми, а не квадратными или треугольными. Кстати, колесо является одним из самых великих изобретений человечества. Согласно археологическим исследованиям первое колесо было изобретено в V тысячелетии до н. э.
Рассмотрим ещё одно интересное свойство окружности. Возьмём верёвочку, свяжем её в кольцо и положим на плоскость. Теперь сделаем из этого кольца разные фигуры: квадрат, треугольник, окружность.
Площадь, ограниченная окружностью (то есть площадь круга), наибольшая среди полученных таким образом площадей.

Отметим, что окружность – это замкнутая кривая линия. Она имеет длину. А круг – плоская фигура, его характеризует площадь.
Кругом называют часть плоскости, которая лежит внутри окружности вместе с самой окружностью.
Окружность – это граница круга. Круг имеет центр, радиус и диаметр. Центром круга называют центр этой окружности. Радиусом и диаметром круга являются, соответственно, радиус и диаметр окружности.
Так, точка О – это центр круга. Отрезок ОК – радиус круга, а отрезок МN – его диаметр.

В начале занятия мы изобразили окружность с помощью циркуля. Наверное, каждый из вас пробовал нарисовать окружность от руки. Скорее всего, получался какой-то овал, отдалённо напоминающий окружность. Конечно, можно потренироваться это делать. Так, великий немецкий художник Альбрехт Дюрер одним движением руки мог настолько точно нарисовать окружность, что даже проверка при помощи циркуля не показывала никаких отклонений.
Бывают случаи, когда нужно нарисовать окружность, а циркуля нет. Если
большая точность не требуется, то можно воспользоваться следующим правилом,
которое записывают в виде трёх пар чисел  ,
,  ,
,  , и
изобразить окружность от руки. Для этого нам понадобится бумага в клетку.
, и
изобразить окружность от руки. Для этого нам понадобится бумага в клетку.
Отметим, что окружность у нас получится определённого размера.
Итак, на пересечении линий клетчатой бумаги поставим точку. Отступив на 3 клетки вправо и на 1 клетку вниз, поставим другую точку. Затем, отступив от второй точки по 1 клетке вправо и вниз, поставим третью точку. И, отступив 1 клетку вправо и 3 клетки вниз, поставим четвёртую точку. Теперь, соединив плавной линией полученные точки, мы получим четверть окружности.
По такому же правилу мы можем дорисовать ещё три четверти и получить окружность.
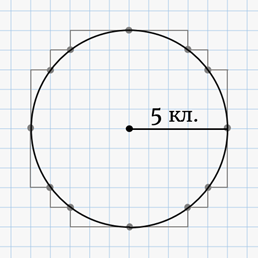
Выше мы отметили, что по такому правилу можно построить окружность определённого размера. Радиус такой окружности равен 5 клеткам.
Для построения окружностей других радиусов таким образом существуют другие правила.
Окружность всегда привлекала к себе внимание художников, архитекторов.
Например, воротам Таврического дворца в Санкт-Петербурге, созданного в конце двадцатого века архитектором Фёдором Ивановичем Волковым, окружности, сплетённые в орнамент, придают особую воздушность.

Окружности и дуги являются основными элементами готических храмов Средневековья.
Архитектура православных храмов включает в себя обязательные элементы купола, арки, округлые своды. Это зрительно увеличивает пространство и создаёт эффект лёгкости.
При создании орнаментов с окружностями часто возникает необходимость разделить окружность на равные части.
Давайте представим, что радиус окружности – это часовая стрелка на
круглом циферблате часов. Пусть начальное положение радиуса – 12 часов. Тогда в
3 часа угол между радиусом и его начальным положением равен  . В 6 часов
угол между радиусом и его начальным положением равен уже
. В 6 часов
угол между радиусом и его начальным положением равен уже  . А вот за 12
часов радиус возвратится в своё начальное положение, описав при этом угол
. А вот за 12
часов радиус возвратится в своё начальное положение, описав при этом угол  .
.

Теперь давайте проведём в окружности с центром в точке О три
радиуса так, чтобы углы между ними были равны  . Эти радиусы
разделят окружность на 3 равные части.
. Эти радиусы
разделят окружность на 3 равные части.
Итак, начертим луч ОА с началом в центре окружности.
Построим с помощью транспортира  . Затем
построим
. Затем
построим  ,
,  .
.

Таким образом, мы разделили нашу окружность на три равные части.
Соединив последовательно точки деления отрезками, получим  , вписанный в
окружность. При этом все его стороны равны, то есть треугольник
, вписанный в
окружность. При этом все его стороны равны, то есть треугольник  – равносторонний.
– равносторонний.
Вообще, вписанным в окружность называется любой треугольник, все вершины которого лежат на этой окружности.
Вписать мы можем и другие многоугольники. Чтобы вписать в
окружность, например, равносторонний пятиугольник, мы проведём в окружности 5
радиусов так, чтобы углы между ними были равны  . Эти радиусы
разделят окружность на 5 равных частей. Соединив последовательно точки деления
отрезками, получим равносторонний пятиугольник, вписанный в окружность.
. Эти радиусы
разделят окружность на 5 равных частей. Соединив последовательно точки деления
отрезками, получим равносторонний пятиугольник, вписанный в окружность.

Равносторонний многоугольник, вписанный в окружность, называется правильным.
А сейчас давайте построим правильный шестиугольник следующим образом. Возьмём 6 правильных равных между собой треугольников. Расположим их рядом так, чтобы у них была общая вершина. Вместе они образуют правильный шестиугольник. Если общую вершину этих треугольников считать центром окружности с радиусом, равным стороне треугольника, то остальные вершины треугольников окажутся на окружности. Получаем, что правильный шестиугольник вписан в окружность и все его стороны равны радиусу этой окружности.

Зная это, можно вписать правильный шестиугольник в окружность без транспортира, пользуясь только циркулем.
Построим окружность некоторого радиуса и отметим на ней произвольную точку. Затем, не меняя раствора циркуля, разделим окружность на 6 равных частей. Соединим последовательно точки деления и получим правильный шестиугольник, вписанный в окружность.

Обратите внимание, если соединить точки деления окружности через одну, то получим правильный треугольник, вписанный в окружность.
А теперь давайте выполним задание. Начертите окружность радиусом 3 см с центром в точке О. Вычислите диаметр окружности.
Решение.



 Получите свидетельство
Получите свидетельство Вход
Вход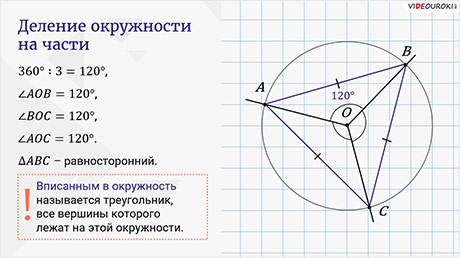




 3002
3002


