Механическая работа и мощность. Энергия

На прошлом уроке мы с вами говорили об импульсе тела. А также смогли сформулировать второй закон Ньютона в импульсной форме, который позволяет нам установить, как изменяется модуль и направление скорости тела, при действии на него силы в течение некоторого промежутка времени. В этом случае говорят, что сила совершает механическую работу.

Таким образом, механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы. Тогда же мы говорили о том, что если под действием постоянной силы тело двигается прямолинейно и совершает перемещение в направлении действия силы, то сила совершает работу, равную произведению модуля этой силы и модуля перемещения:

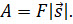
Из определения следует единица измерения работы в метрической системе единиц — ньютон, умноженный на метр:

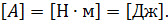
Эта единица была названа джоулем, в честь английского учёного Джеймса Джоуля, впервые экспериментально обосновавшего эквивалентность работы и теплоты.

Мы вспомнили самый простой случай, когда перемещение тела и сила, действующая на него, совпадают по направлению. Теперь давайте вспомним, как вычисляется работа, когда направление действия силы не совпадает с направлением перемещения тела. Итак, у нас есть блок, через который перекинута нить. К одному концу нити прикреплён брусок известной массы. На этот брусок действуют всего две — сила тяжести, направленная вертикально вниз, и сила натяжения нити, направленная вверх вдоль нити.

Если мы равномерно потянем за нить, то брусок начнёт равномерно двигаться. Следовательно, результирующая сила, действующая на брусок, будет равна нулю. Значит, при некотором перемещении тела работа результирующей силы тоже будет равна нулю. Однако сила натяжения нити совершает работу, причём работу положительную, так как её направление совпадает с направлением перемещения тела. А поскольку при равномерном движении сила натяжения нити по модулю равна силе тяжести бруска, то можно предположить, что сила тяжести совершает такую же по величине работу, но отрицательную. Отсюда мы можем сделать достаточно простой вывод: работа силы может быть положительной, отрицательной или равной нулю.

И давайте рассмотрим наиболее общий случай вычисления работы. Итак, у нас есть трактор, который передвигает бетонный блок, действуя на него постоянной силой. Как видно из рисунка, сила тяги составляет некоторый угол с направлением перемещения блока. Разложим эту силу  на две составляющие: перпендикулярную перемещению  и параллельную ему .

В направлении перпендикулярной составляющей силы тяги блок не перемещается. Значит эта сила работы не совершает. Следовательно, работа силы тяги равна работе её составляющей, которая направлена по движению блока. Именно эта проекция и определяет действие силы, изменяющей скорость тела по модулю:

Из прямоугольного треугольника видно, что проекция силы на вектор перемещения равна

Тогда можно записать, что работа постоянной силы равна произведению модуля этой силы на модуль перемещения и на косинус угла между ними:

Это и есть общее выражение для работы постоянной силы.

Из него следует, что процесс совершения работы возможен только при наличии силы, приложенной к телу, и перемещения тела под действием этой силы.

Несмотря на то, что в общем случае перемещения разных точек твёрдого тела различны, при определении работы мы под перемещением будем понимать перемещение точки приложения силы.

Из формулы для работы также видно, что в случае, когда угол между направлением вектора силы и вектора перемещения острый, то работа этой силы считается положительной. Если вектор силы и вектор перемещения составляют между собой тупой угол, то значение косинуса этого угла будет меньше нуля. Значит и работа этой силы будет отрицательна. И, наконец, если вектор силы перпендикулярен вектору перемещения, то работа не совершается (точнее сказать, работа этой силы равна нулю).

Ещё раз обратим внимание на тот факт, что если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работ, совершаемых отдельными силами (или, говорят, равна работе равнодействующей силы):

Механическую работу можно представить в виде графика зависимости проекции силы от координаты тела. Для примера рассмотрим движение тела вдоль оси Оx под действием постоянной силы, направление которой совпадает с направлением перемещения.

Очевидно, что проекция этой силы на ось Оx также постоянна и положительна. Значит её график будет располагаться в первой четверти. И это будет прямая линия, параллельная оси координат. А работа этой силы численно равна площади закрашенного прямоугольника.

Если же сила изменяется в процессе движения, то её работу можно представить, как произведение средней силы на модуль перемещения. В частности, если сила меняется линейно на данном перемещении, то её работа равна площади заштрихованной трапеции.

Отметим ещё и тот факт, что механическая работа зависит от выбора системы отсчёта. Для примера представим, что мы находимся в снижающемся вертолёте и нам надо определить, какую работу совершает действующая на нас сила тяжести. Так вот, если систему отсчёта мы свяжем с вертолётом, относительно которого мы покоимся, то сила тяжести работу совершать не будет. Однако в системе отсчёта, связанной с Землёй, мы движемся (причём в направлении действия силы). Поэтому сила тяжести будет совершать положительную работу.

Как вы знаете, одна и та же работа в разных случаях может быть выполнена за различные промежутки времени. То есть она может совершаться неодинаково быстро. При этом очевидно, что чем меньшее времени требуется для выполнения данной работы, тем эффективнее работает машина, механизм и прочее.

Скалярная физическая величина, характеризующая быстроту совершения работы, и равная отношению работы, совершаемой силой, к промежутку времени, в течение которого она совершается, называется мощностью:

Исходя из определения видим, что единицей измерения мощности является джоуль, делённый на секунду. Эта единица получила название ватт, в честь английского учёного Джеймса Уатта — изобретателя универсального парового двигателя.

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду:

А, например, мощность автомобильных двигателей до сих пор указывают во внесистемной единице — лошадиных силах (1 л. с. = 736 Вт).

Как мы уже не раз говорили, при движении любого тела на него, в общем случае, действует несколько сил. И каждая из этих сил совершает работу. Например, постоянная сила, под действием которой тело движется равномерно и прямолинейно, совершает работу, равную произведению модуля этой силы на модуль перемещения и на косинус угла между ними:

Тогда мощность этой силы равна отношению работы силы к промежутку времени:

Так как отношение модуля перемещения к промежутку времени, за который оно произошло, — это модуль скорости тела, то для постоянной силы и скорости мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.

По записанной формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значение средней или мгновенной скорости.

Из полученной формулы следует, что при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения. Вот почему, например, во время пахотных работ, когда нужна наибольшая сила тяги, трактористы двигаются с небольшой скоростью.