Третий закон Ньютона. Инерциальные системы отсчёта

На прошлых уроках мы с вами выяснили, что любое действие тел друг на друга носит характер ВЗАИМОДЕЙСТВИЯ. Проще говоря, не бывает одностороннего действия одного тела на другое.

Давайте вспомним, что количественной мерой воздействия одного тела на другое является сила. Именно она является причиной возникновения ускорения тела или его деформации.

Примеров взаимодействия тел и сообщения ими друг другу ускорений можно привести очень много. Например, если вы, находясь в одной лодке, будете притягивать к себе за канат другую лодку, то и ваша лодка обязательно придёт в движение.

Но действия тел друг на друга обнаруживаются не только при их непосредственном контакте. Для примера установим на одну лёгкую и подвижную тележку магнит, а на вторую — металлический брусок. Если тележку с бруском удерживать на одном месте, а с магнитом отпустить, то мы заметим, как последняя начнёт двигаться в сторону металлического бруска.

Вернём тележку в исходное состояние и повторим опыт, но в этот раз будем удерживать тележку с магнитом. Как видим, теперь тележка с бруском пришла в движение.

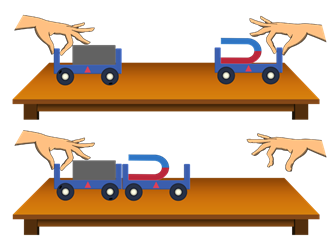
Теперь подумаем, а одинаковы ли модули сил, с которыми магнит и брусок притягиваются друг к другу? Для ответа на этот вопрос немного видоизменим опыт, прикрепив к концам тележек две одинаковые пружины, вторые концы которых жёстко закреплены.

Нетрудно заметить, что после остановки тележек пружины, удерживающие их, растянуты совершенно одинаково. Это свидетельствует о том, что на оба тела со стороны пружин действуют одинаковые по модулю силы, но направлены они противоположно друг другу. А так как магнит и брусок покоятся, то силы, с которыми они действуют друг на друга, также равны по модулю и противоположны по направлению.

Результаты наших опытов не случайны. Они ещё раз доказывают, что механическое действие тел друг на друга всегда взаимно — это либо взаимное притяжение, либо взаимное отталкивание. Одностороннего действия не бывает: существует лишь ВЗАИМОДЕЙСТВИЕ.

Ньютон в своём великом труде «Математические начала натуральной философии» так сформулировал свой третий закон: «Действию всегда есть равное и противоположное противодействие, иначе взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны».

Если учесть, что под словами «действие» и «противодействие» Ньютон понимал силы, с которыми взаимодействуют тела, то третий закон Ньютона может быть переформулирован так: силы, с которыми взаимодействующие тела действуют друг на друга, направлены по одной прямой, равны по модулю и противоположны по направлению.

Третий закон Ньютона справедлив для тел любых масс, размеров, форм и состава вещества. В связи с этим может возникнуть логичный вопрос: «Почему, например, тогда во время прыжка мы движемся вверх, а земля при этом вниз не движется?» Всё очень просто. Вот у нас есть Земля, с её огромной массой, а вот мы — крохотное существо на её поверхности. Во время прыжка мы отталкиваемся с силой, которая действует и на нас, и на Землю. Тогда, согласно второму закону Ньютона, наша маленькая масса во время взаимодействия должна получить большое ускорение. В то время как Земля, с её огромной массой, получит очень крошечное ускорение, которое мы даже не замечаем. Давайте дадим этому ускорению приближённую оценку. Для этого предположим, что во время прыжка мы поднялись на высоту 20 см за 1 с. Тогда, согласно формулам кинематики, приобретённое нами ускорение составило 0,4 м/с².

Теперь предположим, что наша масса равна 50 кг, а значение массы Земли мы возьмём из таблицы. Тогда найдём, что ускорение, которое приобретает Земля, примерно равно 0,3 ∙ 10^–25 м/с²!

Таким образом, видим, что равенство сил не означает равенства результатов их действия.

Теперь обратим внимание ещё на некоторые важные моменты, вытекающие из третьего закона Ньютона. Во-первых, силы, которые возникают при взаимодействии тел, приложены к разным телам, и поэтому они не могут уравновешивать друг друга. А во-вторых, силы, с которыми тела действуют друг на друга, одной физической природы. Например, планета и её спутник взаимодействуют друг с другом силами всемирного тяготения. А магнит и металлический брусок — посредством сил электромагнитного взаимодействия.

При изучении первого закона Ньютона мы с вами отмечали, что все законы движения и взаимодействия тел, которые мы уже знаем и будем изучать в дальнейшем, сформулированы для инерциальных систем отсчёта, так как в них они имеют самый простой вид.

Давайте с вами вспомним, что инерциальными называются системы отсчёта, в которых тело, при компенсации внешних воздействий, покоится или движется равномерно и прямолинейно. Их существование постулируется в первом законе Ньютона — законе инерции. Из его формулировки следует, что если известна из опыта хотя бы одна инерциальная система отсчёта, то инерциальными будут любые другие системы отсчёта, движущиеся относительно избранной равномерно и прямолинейно. В этом заключается их принцип равноправности.

И напротив, любая система отсчёта, движущаяся с ускорением относительно инерциальной, считается неинерциальной системой отсчёта.

При решении большинства задач мы условились инерциальную систему отсчёта связывать с Землёй. Это так называемая геоцентрическая система отсчёта. Однако вам известно, что Земля не только вращается вокруг своей оси, но и обращается вокруг Солнца почти по круговой орбите. Значит, она движется с ускорением. Поэтому, строго говоря, система отсчёта, связанная с нашей планетой, не является инерциальной. Но отличие этой системы от инерциальной будет очень небольшим, так как за те небольшие интервалы времени, за которые мы проводим эксперименты, дугу орбиты, по которой движется Земля, можно с большой точностью считать отрезком прямой линии. Ускорение, возникающее из-за вращения Земли, тоже очень мало́ (оно составляет всего около 0,35 % от ускорения свободного падения). Поэтому с точностью, необходимой для проведения наших экспериментов, мы можем считать систему отсчёта, связанную с Землёй, инерциальной. Как правило, в ней в качестве начала координат выбирается центр Земли в соответствии с принятой её моделью. Ось z совпадает с осью вращения земли. А оси x и y находятся в экваториальной плоскости.

Однако, если требуется большая точность (например, при расчётах движений космических аппаратов), то инерциальной можно считать гелиоцентрическую систему отсчёта. В ней точка отсчёта совмещается с центром Солнца, а координатные оси направляются на удалённые звезды.

Как выбор системы отсчёта сказывается на характере движения тела, посмотрим на примере колебания маятника. Для простоты поместим его на полюс Земли. Пусть маятник у нас будет идеальным и на него действуют только две силы — сила притяжения к Земле и сила упругости нити маятника. Согласно второму закону Ньютона, ускорение маятника совпадает с направлением равнодействующей силой и поэтому лежит в той же вертикальной плоскости. Следовательно, в инерциальной системе отсчёта плоскость колебаний должна оставаться неизменной. Так и будет происходит в гелиоцентрической системе.

А вот в геоцентрической системе отсчёта, являющейся в данном случае неинерциальной, колебания маятника будут выглядеть совершенно иначе. Дело в том, что из-за вращения Земли плоскость колебаний маятника будет поворачиваться. И это смещение становится заметным уже спустя несколько минут наблюдения

Впервые этот опыт был продемонстрирован французским физиком Жаном Фуко во время публичной демонстрации под куполом Пантеона в Париже в 1851 году. Поэтому такой маятник принято называть маятником Фуко. Его часто используют для демонстрации суточного вращения Земли.

Теперь познакомимся с ещё одним важным положением механики — принципом относительности Галилея. Галилей впервые обратил внимание на то, что равномерное и прямолинейное движение по отношению к Земле не сказывается на протекание механических процессов.

Проведём мысленный эксперимент, подобный эксперименту Галилея. Представьте, что вы находитесь на земле и играете в мяч, подбрасывая его вверх. Движение мяча достаточно простое: сначала он замедленно летит вверх, а после — ускоренно падает вниз. Траектория — прямая линия. Переместимся в каюту корабля или вагон поезда, или в кузов грузовика, движущихся равномерно и прямолинейно, и повторим опыт. С мячом ничего сверхъестественного не происходит: он также сначала он замедленно летит вверх, а после — ускоренно падает вниз. Траекторией является всё та же прямая линия. Другими словами, во всех инерциальных системах отсчета механические явления при одинаковых условиях происходят одинаково.

Галилей первым обратил внимание на эту закономерность и заключил, что «для предметов, захваченных равномерным движением, это движение как бы не существует».

Так был сформулирован принцип относительности Галилея. В настоящее время он звучит так: во всех инерциальных системах отсчёта все механические явления при одинаковых начальных условиях происходят одинаковым образом.

Это утверждение выражает равноправие всех инерциальных систем в механике: никакой механический эксперимент не в состоянии выделить и сделать главной какую-то одну инерциальную систему отсчёта по сравнению с остальными.

Однако не следует думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела в разных инерциальных системах отсчёта. Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными условиями. А они могут отличаться. Вспомните хотя бы мысленный опыт Галилея по сбрасыванию ядра с вершины мачты корабля, который движется равномерно по реке. Для наблюдателя, находящегося на палубе, траекторией движения ядра является прямая линия. А путь и модуль перемещения ядра будут равны.

Но с точки зрения наблюдателя, находящегося на берегу, ядро будет двигаться по параболе, так как оно имеет некоторую начальную горизонтальную скорость, равную скорости корабля. А модуль его перемещения не будет равен пройденному пути.

Физические величины, которые будут изменяться при переходе из одной инерциальной системы отсчёта в другую, мы будем называть относительными.

Если же физические величины не изменяются при переходе из одной инерциальной системы отсчёта в другую (например, масса и сила), то их называют инвариантными.

И действительно, сила, с которой мяч ударяется о землю, не зависит от того, кто наблюдал за этим ударом: человек, стоящий возле мяча или который в это время проезжал рядом с постоянной скоростью.

Или вот масса космонавта будет одинакова и на Земле, и на Луне, и на Сатурне с Ураном

Открытие принципа относительности — одно из величайших достижений человечества. Но оно оказалось возможным лишь после того, как люди поняли, что ни Земля, ни даже Солнце не являются центром Вселенной.

В заключение отметим, что три закона Ньютона, лежащие в основе классической механики, выполняются для тел, скорость которых намного меньше скорости света в вакууме. В процессе развития физики, изучая движение микроскопических объектов при скоростях, сравнимых со скоростью света, обнаружили, что в этом случае законы Ньютона не выполняются. Теорией, описывающей не только медленные, но и быстрые движения частиц, является специальная теория относительности, основы которой разработаны Эйнштейном в 1905 году. Однако о ней мы с вами будем говорить значительно позднее.