Точность и погрешность измерений

Вы всегда можете точно сказать, сколько учеников в вашем классе или сколько конфет в коробке, которую вам подарили на день рождения. Также вам не сложно будет подсчитать деревья, которые растут в сквере.

Но всё же чаще всего измерения или подсчёты невозможно выполнить абсолютно точно, так как возникают неизбежные погрешности, то есть случайные отклонения от истинного значения.

Главный источник погрешности – изменчивость измеряемой величины. Кроме того, погрешностью обладает измерительный инструмент.

Давайте поговорим о погрешности на примере числа жителей города.

В 2021 году в России было 15 городов с числом жителей более 1 млн человек.

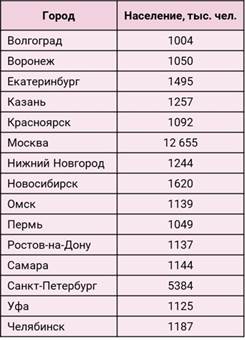
Обратите внимание, что в этих данных единицей измерения служит тысяча человек. Конечно же, мы понимаем, что число жителей городов в этой таблице дано приближённо и что истинное число жителей, скорее всего, не кратно тысяче.

Но что понимать под истинным числом жителей города? Ведь в течение года люди всё время приезжают и уезжают, кто-то рождается, а кто-то умирает. А значит, число жителей города не постоянно и меняется на протяжении года каждый день. Но вот число тысяч людей, населяющих крупный город, скорее всего, за день не изменится. Поэтому данные в таблице даны в тысячах человек. Более высокая точность подсчётов в данном случае не имеет смысла из-за изменчивости числа жителей.

Отметим, что в данных Российской службы статистики можно встретить измерения численности населения городов с точностью до одного человека. Это объясняется тем, что данные не округляются. При этом обычно указывается метод, с помощью которого проведён пересчёт.

Теперь поговорим о погрешности на примере роста человека.

Говоря о росте человека, мы округляем данные до сантиметра. Так измеряют рост в России и в континентальной Европе. А вот в Соединённых Штатах Америки, Великобритании, Австралии и некоторых других странах рост измеряется в дюймах. Считается, что 1 дюйм равен 2,54 сантиметра.

Дюйм – голландское слово, которое означает «большой палец». Изначально за дюйм принималась длина первой фаланги большого пальца руки.

Также один дюйм определяли как длину трёх ячменных зёрен.

Наверное, каждый из вас читал сказку про Дюймовочку. Теперь вы представляете, какой миниатюрной она была, ведь её рост был равен всего лишь 1 дюйму.

Рост человека редко равен целому числу сантиметров или дюймов. Конечно, его нетрудно измерить с большей точностью, но в этом нет необходимости. Ведь для практических нужд, например, для пошива одежды, определения размеров мебели или сидений в автомобилях достаточно измерений с точностью до сантиметра или дюйма.

Кроме того, рост человека не остаётся постоянным в течение суток (утром рост человека чуть больше, чем вечером), так как за день под влиянием нагрузки хрящи в суставах несколько сжимаются, а за ночь, когда человек лежит, вновь расправляются.

Ещё один пример не вполне точно определённой величины – это расстояние между городами.

Мы с вами понимаем, как измерить расстояние между двумя точками вдоль некоторой линии. Но город – это не точка, а некоторая территория. К тому же граница города не всегда отчётлива. А значит, расстояние между городами точно определить не получится. Кроме того, расстояние между городами обычно измеряют не по прямой линии, а вдоль шоссе или железной дороги.

В России за расстояние между городами принимают расстояние между их центральными почтовыми отделениями вдоль главных дорог. Этот способ определения расстояния появился одновременно с регулярной почтовой службой.

Расстояние между городами измеряют с точностью до километра. Для практических целей, например, чтобы рассчитать время в пути или расход горючего, этого вполне достаточно.

Приведённые примеры говорят о том, что выбирать точность измерения изменчивых величин нужно так, чтобы погрешность не влияла на последующие выводы. Слишком высокая точность не нужна, а иногда даже вредна. Излишне точные измерения отнимают время, силы и даже могут порождать ошибки.

Тем не менее измерительные приборы должны обеспечивать необходимую точность. Допустимая погрешность измерительного прибора определяется стандартом.

Перед вами таблица, в которой приведена допустимая погрешность весов при эксплуатации.

Это весы III класса точности, то есть не очень точные. Они рассчитаны на груз от 20 кг до 3000 кг.

В соответствии с ГОСТ весы имеют разные допустимые погрешности при разной нагрузке.

Знак «±» означает, что отклонение возможно в любую сторону – и в меньшую, и в большую. Например, если на таких весах взвешивается груз массой ровно 555 кг, то они могут показать от 553 кг до 557 кг. Если же весы показали, что груз имеет массу 555 кг, то истинная масса груза находится в пределах от 553 кг до 557 кг.

Это можно выразить двойным неравенством 553 кг  557 кг.

У лабораторных весов допустимые погрешности намного меньше. Например, точные лабораторные весы могут иметь допустимую погрешность всего лишь 0,001 г.

Мы привели пример абсолютной погрешности, которая показывает разность между истинным значением и приближённым. Иногда погрешности измеряются в процентах самой величины. Давайте посмотрим на катушку швейных ниток.

К катушке прикреплён ярлык, запись на котором означает, что истинная длина нитки находится в пределах от 200 ∙ 0,95 = 190 (м) до 200 ∙ 1,05 = 210 (м). Это удобно записать двойным неравенством 190 м  210 м, где  – истинная длина нитки.

Сегодня мы выяснили, что точность измерения для разных величин должна быть разной. А также узнали, что слишком большая точность может быть даже вредна.

До встречи на следующих занятиях!