Сложение и вычитание смешанных чисел

Сегодня на уроке мы научимся складывать и вычитать смешанные числа.

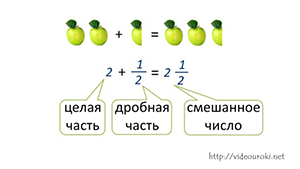
Напомним, сумму натурального числа и правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. То есть «смешали» натуральное число и правильную дробь, и назвали эту запись смешанным числом.

Натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.

То есть запись  является сокращённым вариантом записи .

Складывать смешанные числа помогают свойства сложения: переместительное и сочетательное.

Пример

Найдём сумму чисел  и .

При выполнении записи в тетрадях, не нужно записывать смешанное число как сумму натурального числа и дроби, затем подробно расписывать, как вы складываете целые и дробные части смешанных чисел.

Пример

Найдём сумму смешанных чисел  и .

Таким образом, если при сложении дробных частей получилась неправильная дробь, выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.

Пример

Теперь найдём сумму чисел  и .

Задача

На столе лежало  пиццы. Если принести ещё  пиццы. Сколько пицц окажется на столе?

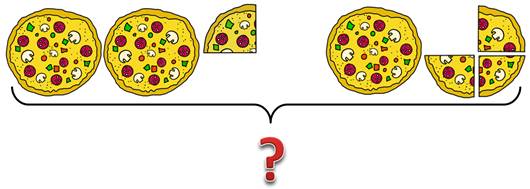
Чтобы решить задачу, надо сложить числа  и .

Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.

Пример

Вычтем из дроби  дробь .

Есть в вычитании «коварные» примеры.

Пример

Запомните! Не начинайте выполнять вычитание, пока не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби.

А вот если вычесть нельзя, «занимаем» у целой части уменьшаемого одну целую единицу.

Иногда в примерах нужно вычесть из натурального числа смешанную дробь.

Пример

Найдём значение выражения .

Итоги

Чтобы сложить смешанные числа, надо: привести дробные части этих чисел к наименьшему общему знаменателю; отдельно выполнить сложение целых частей и отдельно дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части.

Чтобы выполнить вычитание смешанных чисел, надо: привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей.