Видеоучебник / Физика / Решение задач по физике. Механика 7-11 класс. / Силы упругости. Закон Гука

Новогодняя распродажа готовых материалов для учителей! Скидки до 50 %

Силы упругости. Закон Гука

Урок 12. Решение задач по физике. Механика 7-11 класс.

На этом занятии мы предлагаем Вам разбор решения четырех задач с использованием закона, экспериментально установленным Робертом Гуком. В ходе решения одной из задач, мы выведем формулы для жесткости пружин, соединенных последовательно и параллельно.

Конспект урока "Силы упругости. Закон Гука"

«Напичканный знаниями, но не умеющий

их использовать ученик, напоминает

фаршированную рыбу, которая не может плавать».

А.Л. Минц

Данная тема будет посвящена решению задач на силы упругости и закон Гука.

Задача 1. Две пружины равной длины поочередно растягиваются под действием одной и той же силы. Пружина жесткостью 500 Н/м растянулась на 1 см. Чему равна жесткость второй пружины, если ее растяжение равно 5 см?

ДАНО:

РЕШЕНИЕ:

Записываем III закон Ньютона для 1-ой и 2-ой пружины:

В проекциях на ось Оy:

По условию задачи F₁ = F₂, то получаем

Тогда жёсткость второй пружины равна

Ответ: 100 Н/м.

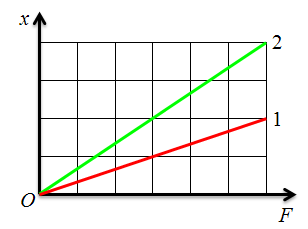
Задача 2. На рисунке изображены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и радиуса. Сравните жесткости проволок.

ДАНО:

РЕШЕНИЕ:

По третьему закону Ньютона:

По закону Гука:

Т.к. по условию задачи силы F₁ и F₂ равны, то

Ответ: жесткость стальной проволоки в 2 раза больше жесткости медной проволоки.

Задача 3. Две одинаковые пружинки одинаковой жесткости соединяют в первом случае последовательно, а во втором — параллельно. В каком случае и во сколько раз жесткость составной пружины будет больше?

ДАНО:

РЕШЕНИЕ:

Рассмотрим первый случай, когда пружины соединяют последовательно. Модуль результирующей силы упругости

Модуль полной деформации:

Тогда:

Теперь рассмотрим параллельное соединение пружинок. И так, при параллельном соединении произойдет перераспределение нагрузки в зависимости от жесткости пружин, вследствие чего модуль результирующей силы упругости составной пружины будет равен сумме модулей сил упругости отдельных пружинок

Модуль полной деформации:

Тогда

Следовательно

Задача 4. На подставке лежит груз массой 0,5 кг, связанный с прикрепленной к потолку невесомой пружинкой. В начальный момент времени пружинка не растянута. Подставку начинают опускать с ускорением 0,5g. Через какой промежуток времени груз оторвется от подставки, если жесткость пружинки составляет 5 Н/м?

ДАНО: