Переменный электрический ток. Резистор в цепи переменного тока

В идеальном колебательном контуре, то есть в контуре без активного сопротивления, возникающие электромагнитные колебания могут существовать бесконечно долго. Однако в реальных контурах всегда имеется нагрузка, обладающее сопротивлением. Поэтому часть энергии контура всегда превращается во внутреннюю энергию проводников. Проще говоря, реальные электромагнитные колебания в контуре являются затухающими. Для того чтобы они были незатухающими, необходимо компенсировались потери энергии при каждом полном колебании в контуре.

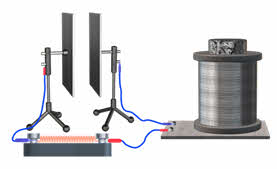
Давайте с вами вспомним, что для механических колебаний это достигалось путём воздействия внешней периодической силы. В результате в системе возникали вынужденные колебания. Аналогично этому вынужденные электромагнитные колебания в колебательном контуре происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения. При этом напряжение в цепи и сила тока изменяются как по знаку, так и по модулю.

Ток, сила и направление которого периодически меняются, называется переменным.

В настоящее время основная часть электроэнергии в мире вырабатывается с помощью электромеханических индукционных генераторов переменного тока, создающими синусоидальное напряжение.

Индукционным генератором переменного тока называется устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

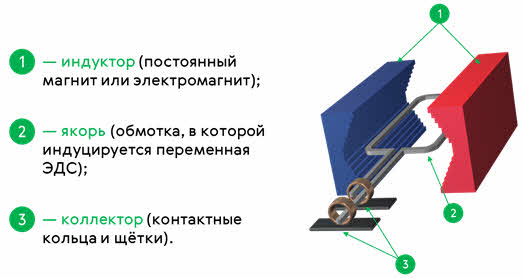
Как следует из названия устройства, принцип действия такого генератора основан на явлении электромагнитной индукции. Основными частями индукционного генератора переменного тока являются:

индуктор — это постоянный магнит или электромагнит, который создаёт магнитное поле;

якорь — это обмотка, в которой индуцируется переменная ЭДС;

и колле́ктор — это контактные кольца и скользящие по ним контактные пластины (щётки). С помощью коллектора ток снимается или подводится к вращающимся частям.

Давайте рассмотрим принцип действия простейшего индукционного генератора на примере проводящей рамки с током, вращающейся в однородном магнитном поле с постоянной угловой скоростью.

Пусть в начальный момент времени угол между нормалью к плоскости рамки и линиями индукции магнитного поля равен нулю. Так как рамка вращается с постоянной угловой скоростью, то данный угол будет меняться с течением времени по линейному закону:

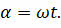
Тогда будет меняться и магнитный поток через поверхность, ограниченную плоскостью рамки:

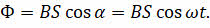
Поскольку магнитный поток, пронизывающий рамку, изменяется со временем, то в ней согласно закону Фарадея индуцируется ЭДС индукции, равная первой производной магнитного потока по времени, взятой с обратным знаком:

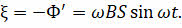
Произведение величин, стоящих перед функцией синуса есть ничто иное, как амплитудное значение ЭДС индукции:

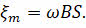
Отсюда следует, что изменение ЭДС индукции в контуре со временем происходит по закону синуса:

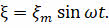
Это достаточно легко проверить, если подключить выводы вращающейся рамки к осциллографу. Нетрудно увидеть, что временная развёртка представляет собой синусоиду.

Если к выводам рамки подключить нагрузку с достаточно большим сопротивлением (намного большим, чем сопротивление рамки), то по ней будет проходить переменный ток.

По закону Ома для полной цепи его сила будет также изменяться по синусоидальному закону:

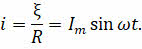
Анализируя последние два выражения, мы можем сделать вывод, что в цепи, содержащей, кроме рамки, только сопротивление, колебания напряжения и колебания силы тока совпадают по фазе, одновременно достигая максимумов и минимумов.

Однако в общем случае (например, когда в цепи присутствует конденсатор, или катушка, или то и другое одновременно) колебания силы тока в цепи и напряжения будут происходить с одинаковой частотой, но не будут совпадать по фазе:

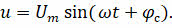
Ещё раз обратим ваше внимание на то, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остаётся неизменным в течение следующего полуоборота.

Промежуток времени, в течение которого ЭДС совершает одно полное колебание, называется периодом переменного тока.

А число полных колебаний за одну секунду называется частотой тока.

В электрических сетях большинства стран мира (в том числе и в России) стандартная частота переменного тока равна 50 Гц. Продолжительность периода такого тока составляет всего 0,02 с. Такая частота переменного тока была выбрана с участием известного немецкого электротехника польско-русского происхождения Михаила Осиповича Доливо-Добровольского.

Однако, например, в США, Канаде и некоторых других странах по рекомендации известного сербского учёного Николы Тесла, стандартная частота переменного тока равна 60 Гц.

Мы рассмотрели на схеме принцип работы генератора переменного тока. Однако такой тип генераторов (с неподвижной магнитной системой и вращающимся якорем) используется достаточно редко. Дело в том, что при помощи подвижных контактов практически невозможно отводить от генератора ток высокого напряжения из-за сильного искрения в контактах. Поэтому почти во всех индукционных генераторах переменного тока якорь, в котором индуцируется ЭДС, устанавливают неподвижно, а вращаться заставляют индуктор.

Вращающаяся часть генератора называется ротором. Он располагается внутри неподвижной стальной станины цилиндрической формы, называемой статором. Во внутренней части статора имеются специальные пазы, в которые укладывается медный провод в виде витков. При вращении ротора в этих витках и индуцируется переменный ток.

Ротор также имеет сложную форму и представляет собой стальной сердечник с навитой на него обмоткой. По обмотке пропускается постоянный ток, который подводится через щётки и кольца от постороннего источника постоянного тока. Создаваемое этим током магнитное поле вращается вместе с ротором. При этом силовые линии поля будут пересекать проводники, вложенные в пазы статора, и индуцировать в них ЭДС.

Современные мощные генераторы вырабатывают напряжение до 15—20 кВ, а их коэффициент полезного действия может достигать 97—98 %.

Теперь давайте рассмотрим некоторые новые закономерности, которые возникают в электрической цепи при её подключении к источнику переменного тока. Итак, пусть источник создаёт переменно напряжение, изменяющееся со временем по закону синуса:

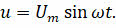
По закону Ома для участка цепи, содержащим только сопротивление, сила тока во всей цепи будет также изменяться по гармоническому закону:

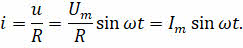
Максимальные величины напряжения и силы тока называются амплитудными значениями напряжения и силы тока соответственно.

А значения напряжения и силы тока в любой момент времени называются мгновенными.

Зная их, можно рассчитать мгновенную мощность переменного тока, которая, в отличие от цепей постоянного тока, изменяется с течением времени:

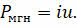
Под средней за период мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

С учётом зависимости силы тока от времени перепишем выражение для мгновенной мощности на резисторе в цепи переменного тока:

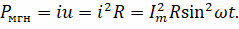
Поскольку мгновенная мощность изменяется со временем, то использовать эту величину на практике в качестве характеристики длительно протекающих процессов очень неудобно. Давайте перепишем нашу формулу для мощности немного по-другому (воспользовавшись знаниями из математики):

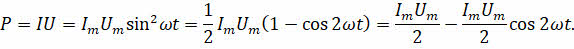
Как видим, в полученном уравнении первое слагаемое не зависит от времени. А второе слагаемое — это переменная составляющая, являющаяся функцией двойного угла. Её среднее значение за период (или время, кратное периоду) равно нулю, поскольку половину периода косинус принимает положительные значения, а вторую — отрицательные. Поэтому среднее значение мощности переменного тока за время, большее чем период колебаний, можно найти как половину произведения амплитудных значений силы тока и напряжения, или половину произведения квадрата амплитудного значения силы тока и сопротивления:

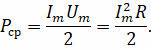
Таким образом, сопротивление играет двоякую роль в цепи переменного тока. Во-первых, оно ограничивает силу тока. А во-вторых, на активном сопротивлении происходит безвозвратное превращение электроэнергии в другие виды (в частности, во внутреннюю).

Выражение для средней мощности позволяет ввести действующие или эффективные значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.

Действующее значение силы переменного тока равно силе такого постоянного тока, который, проходя в электрической цепи по активному сопротивлению, выделяет за промежуток времени, кратный периоду колебаний, такое же количество теплоты, что и данный переменный ток.

Оно численно равно квадратному корню из среднего за период значения квадрата силы переменного тока:

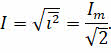
Аналогично можно ввести действующее значение для напряжения и ЭДС:

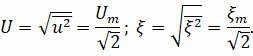
Амперметры и вольтметры регистрируют именно действующие значения силы тока и напряжения.

Для закрепления материала, решим с вами одну небольшую задачу. Квадратная рамка площадью 500 см² вращается в однородном магнитном поле с индукцией 10 мТл вокруг оси, лежащей в плоскости рамки и перпендикулярной полю, совершая 25 оборотов в секунду. Определите действующее значение силы тока в рамке, если её сопротивление равно 5 Ом.

В заключение урока отметим, что закон Ома для участка цепи переменного тока, содержащего только резистор, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока вследствие того, что их колебания совпадают по фазе.

Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии в энергию теплового движения частиц. Вследствие этого сопротивление резисторов получило название активного или омического сопротивления.