Представим себе такую историю…
– Саша, чем ты занимаешься? – спросил у друга Паша.
– Пытаюсь посчитать, сколько корма нужно моему коту Ваське на неделю, – ответил Саша.
– И как ты это собираешься высчитать? – удивился Паша.
–
Я заметил, что каждый день Васька съедает по  пакетика корма, –
продолжил Саша. — Значит, чтобы посчитать, сколько корма понадобится коту
Ваське на неделю, нужно к
пакетика корма, –
продолжил Саша. — Значит, чтобы посчитать, сколько корма понадобится коту
Ваське на неделю, нужно к  прибавить
прибавить
 прибавить
прибавить
 прибавить
прибавить
 прибавить
прибавить
 прибавить
прибавить  и ещё раз
прибавить
и ещё раз
прибавить  . Тогда
получается, что за неделю кот Васька съедает
. Тогда
получается, что за неделю кот Васька съедает  пакетика корма
или 2 пакета и
пакетика корма
или 2 пакета и  пакета корма.
пакета корма.
–
Ну и много же он у тебя ест! – заметил Паша. – Смотри: у тебя получилась сумма
из 7 равных слагаемых, а мы уже знаем, что такую сумму можно записать короче с
помощью произведения, то есть нужно просто  умножить на 7.
умножить на 7.
–
Ты хочешь сказать, что произведение  и 7 равно
и 7 равно  ? – решил уточнить
Саша.
? – решил уточнить
Саша.
– Получается так, – задумался Паша. – А давай лучше уточним у Мудряша, как умножают дроби.

– Ребята, прежде чем я вам расскажу об умножении дробей, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на
вопрос «Сколько корма потребуется коту Ваське на неделю?», нужно посчитать,
сколько корма он съест за 7 дней. Так как каждый день Васька съедает одинаковое
количество корма –  пакетика, то
можно семь раз сложить дроби
пакетика, то
можно семь раз сложить дроби  , а можно найти
произведение
, а можно найти
произведение  и 7. Ведь мы
знаем, что действие нахождения суммы одинаковых слагаемых называется
умножением. Тогда получается, что за неделю кот Васька съест
и 7. Ведь мы
знаем, что действие нахождения суммы одинаковых слагаемых называется
умножением. Тогда получается, что за неделю кот Васька съест  или
или  пакетика корма.
пакетика корма.

–
Этот пример иллюстрирует следующее правило, – сказал Мудряш. – Запомните!
Чтобы умножить дробь на натуральное число, надо её числитель умножить на это
число, а знаменатель оставить без изменений. В буквенном виде это правило
записывают так:  . Также верными
являются следующие равенства:
. Также верными
являются следующие равенства:  ,
,  .
.
– А если нужно умножить дробь на дробь, – решили уточнить мальчишки, – то как быть в этом случае?
–
Чтобы лучше разобраться, давайте рассмотрим такой пример, – предложил Мудряш. –
Пусть есть прямоугольник с длиной  дециметра и
шириной
дециметра и
шириной  дециметра. Найдём
площадь этого прямоугольника.
дециметра. Найдём
площадь этого прямоугольника.
–
Это сложная задача, – задумались мальчишки. – Ведь площадь прямоугольника равна
произведению длин его соседних сторон. То есть площадь этого прямоугольника
равна  умножить на
умножить на  , а мы ещё не
умеем умножать дроби.
, а мы ещё не
умеем умножать дроби.
–
Сейчас вы всему научитесь, – улыбнулся Мудряш. – Для начала давайте начертим
квадрат со стороной 1 дециметр. Так как у нашего прямоугольника длина  дециметра, то
разделим одну сторону квадрата на 5 одинаковых частей и закрасим 4 части. Ширина
нашего прямоугольника
дециметра, то
разделим одну сторону квадрата на 5 одинаковых частей и закрасим 4 части. Ширина
нашего прямоугольника  дециметра.
Значит, другую сторону квадрата разделим на 3 равные части и закрасим 2 из них.
Скажите, из скольких частей теперь состоит первоначальный квадрат?
дециметра.
Значит, другую сторону квадрата разделим на 3 равные части и закрасим 2 из них.
Скажите, из скольких частей теперь состоит первоначальный квадрат?
– Так как одну сторону квадрата мы разделили на 5 равных частей, а вторую – на 3, то весь квадрат разделён на 15 одинаковых частей, – ответил Паша.
– Правильно! – согласился Мудряш. – А из скольких частей состоит заданный прямоугольник?
– Прямоугольник состоит из 8 равных частей, – ответил Саша.
–
Хорошо! – продолжил Мудряш. — Нетрудно заметить, что площадь нашего
прямоугольника равна  дм2.
Мы с вами уже говорили, что площадь прямоугольника равна произведению длин его
соседних сторон. Следовательно,
дм2.
Мы с вами уже говорили, что площадь прямоугольника равна произведению длин его
соседних сторон. Следовательно,  умножить на
умножить на  равно
равно  .
.

–
Этот пример иллюстрирует следующее правило, – сказал Мудряш. – Запомните!
Произведением двух дробей является дробь, числитель которой равен
произведению числителей, а знаменатель – произведению знаменателей. В
буквенном виде это правило записывают так:  .
.
– Обычно вначале обозначают произведение числителей и знаменателей, – продолжил Мудряш, – затем производят сокращение и только потом выполняют умножение. В ответе, если это возможно, из дроби выделяют целую часть. Если необходимо найти произведение двух смешанных чисел, то сначала надо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. Давайте потренируемся и найдём произведение следующих дробей.
–
 умножить на
умножить на  , – начал Саша. –
Запишем произведение числителей и знаменателей. Сокращать нам здесь нечего.
Значит, выполним умножение. Получим дробь
, – начал Саша. –
Запишем произведение числителей и знаменателей. Сокращать нам здесь нечего.
Значит, выполним умножение. Получим дробь  .
.
–
Найдём следующее произведение, – продолжил Паша. – Запишем произведение
числителей и знаменателей этих дробей. Можем сократить 13 и 26 на 13, и 5 и 10
на 5. Тогда получим дробь  .
.
–
И найдём последнее произведение, – сказал Саша. – Запишем произведение
числителей и знаменателей дробей. Можно сократить 5 и 5 на 5, и 6 и 6 на 6.
Тогда получим дробь  , или просто 1.
, или просто 1.

– Молодцы! – похвалил ребят Мудряш. – Вы знаете, что для натуральных чисел выполняются переместительное свойство умножения, сочетательное свойство умножения, распределительное свойство умножения относительно сложения и распределительное свойство умножения относительно вычитания.
Эти же свойства умножения верны и для дробей.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание
первое: выполните действия: а)  ; б)
; б)  ; в)
; в)  .
.
Решение: найдём
произведение  . Мы уже знаем: чтобы
умножить дробь на натуральное число, надо её числитель умножить на это число, а
знаменатель оставить без изменений. Сократим 40 и 15 на 5. Получим дробь
. Мы уже знаем: чтобы
умножить дробь на натуральное число, надо её числитель умножить на это число, а
знаменатель оставить без изменений. Сократим 40 и 15 на 5. Получим дробь  . Это неправильная
дробь, так как числитель больше знаменателя. Выделим целую часть. В результате
получим
. Это неправильная
дробь, так как числитель больше знаменателя. Выделим целую часть. В результате
получим  .
.
Перейдём
к следующему произведению  . Запишем
произведение числителей и знаменателей наших дробей. Можем сократить 5 и 5 на 5,
3 и 6 на 3, 2 и 2 на 2. В результате получим дробь
. Запишем
произведение числителей и знаменателей наших дробей. Можем сократить 5 и 5 на 5,
3 и 6 на 3, 2 и 2 на 2. В результате получим дробь  .
.
И
найдём последнее произведение  . Здесь удобно
воспользоваться распределительным свойством умножения относительно сложения. Запишем
произведения числителей и знаменателей дробей. В первом произведении можем
сократить 12 и 12 на 12, во втором – 12 и 8 на 4. Получим сумму дробей
. Здесь удобно
воспользоваться распределительным свойством умножения относительно сложения. Запишем
произведения числителей и знаменателей дробей. В первом произведении можем
сократить 12 и 12 на 12, во втором – 12 и 8 на 4. Получим сумму дробей  и
и  . Приведём дроби к
наименьшему общему знаменателю равному 38. Тогда дополнительный множитель к
первой дроби равен 2, ко второй — 1. Получим сумму дробей
. Приведём дроби к
наименьшему общему знаменателю равному 38. Тогда дополнительный множитель к
первой дроби равен 2, ко второй — 1. Получим сумму дробей  и
и  . Воспользуемся
правилом сложения дробей с одинаковыми знаменателями. Получим дробь
. Воспользуемся
правилом сложения дробей с одинаковыми знаменателями. Получим дробь  . Можем сократить
её на 19. В результате получим дробь
. Можем сократить
её на 19. В результате получим дробь  .
.

Перейдём
к следующему заданию: найдите значение выражения  при
при
 .
.
Решение:
подставим вместо а указанное значение. Вычислим первое произведение. Видим: у
нас множители являются смешанными числами. Значит, представим их в виде
неправильных дробей. Тогда первый множитель равен  , второй –
, второй –  . Запишем
произведение числителей и знаменателей этих дробей. Можем сократить числитель и
знаменатель на 3. Получим дробь
. Запишем
произведение числителей и знаменателей этих дробей. Можем сократить числитель и
знаменатель на 3. Получим дробь  . Это неправильная
дробь, так как числитель больше знаменателя. Выделим целую часть. Получим
. Это неправильная
дробь, так как числитель больше знаменателя. Выделим целую часть. Получим  .
.
Перейдём
ко второму произведению. Второй множитель запишем в виде неправильной дроби  . Выполним
умножение дроби на натуральное число. Получим дробь
. Выполним
умножение дроби на натуральное число. Получим дробь  . Выделим целую
часть и получим
. Выделим целую
часть и получим  .
.
Вычислим
сумму смешанных чисел  и
и  . Помним, что при
сложении смешанных чисел целые части складываем отдельно и дробные части
складываем отдельно. Тогда получим
. Помним, что при
сложении смешанных чисел целые части складываем отдельно и дробные части
складываем отдельно. Тогда получим  . Пока сокращать
ничего не будем.
. Пока сокращать
ничего не будем.
Осталось
вычислить разность смешанных чисел  и
и  . В результате
получим
. В результате
получим 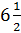 .
.


 Получите свидетельство
Получите свидетельство Вход
Вход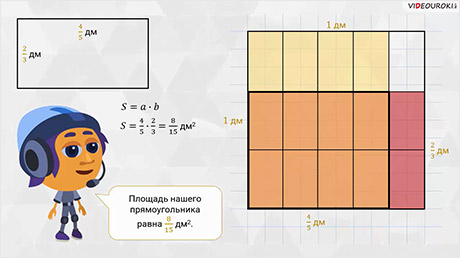



 0
0 3222
3222

