Наверняка вы обращали внимание, что все вокруг находится в движении, однако скорость этого движения различна. Возьмём, к примеру, ледники — они передвигаются крайне неспешно, с ледяным спокойствием проходя всего лишь метр за целую неделю. Спринтеры могут пробежать сто метров приблизительно за 10 секунд. Обычный человек проходит около 5 километров за час. Улитки же полностью соответствуют своей репутации медлительных созданий, преодолевая всего 1,5 миллиметра за одну секунду — это почти в тысячу раз медленнее, чем шагает человек. Так вот, чтобы оценить, как быстро движется тело, в физике применяется физическая величина, называемая скоростью.
Скорость при равномерном прямолинейном движении показывает, какой путь тело проходит за единицу времени. Поскольку при равномерном движении тело за одинаковые промежутки времени проходит одинаковые расстояния, то скорость остаётся постоянной.
Чтобы найти скорость тела при равномерном прямолинейном движении, нужно пройденный путь разделить на время, затраченное на его преодоление:

Как мы помним, путь обозначается латинской буквой s, время — t. А вот скорость обозначается греческой буквой «Ипсилон» (υ). Но читается она латинский манер — как буква «Вэ» (в).
Тогда скорость равномерного прямолинейного движения можно рассчитать по формуле:

Пример с капельницей наглядно демонстрирует, что при равномерном прямолинейном движении скорость остаётся неизменной. С течением времени увеличивается пройденный путь, но сама скорость не меняется.

Таким образом, можно дать другое определение равномерному прямолинейному движению. Равномерное прямолинейное движение — это движение по прямой с постоянной скоростью.
Из формулы скорости легко вывести выражения для нахождения пройденного пути за заданное время, или времени, необходимого для прохождения определённого пути:

Для облегчения запоминания этих формул хитрые ученики пользуются простым правилом. Они располагают величины путь (s), скорость (υ) и время (t) в виде треугольника (как показано на экране), и запоминают их расположение. Затем, если закрыть любой символ в этом треугольнике, можно получить соответствующую формулу.

В Международной системе единиц (СИ) за единицу скорости принимается скорость такого прямолинейного равномерного движения, при котором тело за 1 секунду проходит путь, равный 1 метру. Эта единица называется «метр в секунду»:

На практике нередко используются различные единицы измерения скорости. Например, скорость движения автобусов, поездов или автомобилей удобнее выражать в километрах в час, тогда как скорость космических ракет и спутников чаще указывают в километрах в секунду. Однако в физических расчётах большинство величин принято выражать в основных единицах системы СИ.
Рассмотрим пример перевода скорости из километров в час в метры в секунду. Допустим, велосипедист движется по дороге со скоростью 18 км/ч. Переведём эту величину в метры в секунду.
Для начала вспомним, что в одном километре содержится 1000 метров. А сколько секунд содержится в одном часе? Мы знаем, что в один час — это 60 минут. А одна минута — это 60 секунд. Значит, один час равен 3600 секундам:

Обратный переход от метров в секунду к километрам в час осуществляется аналогичными рассуждениями:

Скорость, помимо численного значения, всегда
имеет направление. Поэтому она является векторной величиной. По этой
причине скорость обозначают как «Вэ со стрелочкой) ( ), а её модуль — без стрелки (υ).
), а её модуль — без стрелки (υ).
Поскольку при прямолинейном движении пройденное телом расстояние равно модулю вектора перемещения, можно утверждать, что векторная физическая величина скорость определяется отношением перемещения тела ко времени, за которое это перемещение произошло:

При прямолинейном движении направление вектора скорости всегда совпадает с направлением движения тела, то есть с направлением вектора перемещения. Когда речь идёт о модуле скорости, мы оцениваем, насколько быстро или медленно перемещается физическое тело. Однако для решения многих задач важно также учитывать направление скорости тела.
Допустим, два автомобиля движутся навстречу друг другу, каждый со скоростью 80 км/ч относительно земли. Тогда относительно друг друга автомобили будут двигаться со скоростью 160 км/ч, потому что их скорости складываются.

Теперь рассмотрим ситуацию, когда автомобиль, движущийся со скоростью 90 км/ч, догоняет другой автомобиль, идущий со скоростью 70 км/ч. В этом случае скорость сближения составляет 20 км/ч — разница скоростей двух автомобилей.

Если же оба автомобиля движутся в одном направлении с одинаковыми скоростями, то относительно друг друга они кажутся неподвижными.
Таким образом, скорость движения тела может быть разной в зависимости от того, какая система отсчёта выбрана для наблюдения.
Пройденный телом путь и его скорость могут меняться со временем. Чтобы лучше показать такие изменения, используют графики. На горизонтальной оси (оси абсцисс) обычно откладывают время. А на вертикальной оси (оси ординат) — пройденный путь или скорость.
Если движение прямолинейное и равномерное, то график зависимости скорости от времени представляет собой прямую линию, параллельную оси абсцисс. Это объясняется тем, что при таком типе движения скорость остаётся неизменной во времени.

График зависимости пройденного пути от времени при прямолинейном равномерном движении выглядит как прямая линия, выходящая из начала координат и проходящая через первую четверть координатной плоскости. С увеличением времени путь, пройденный телом, линейно возрастает, поскольку зависимость между пройденным путём и временем выражается линейной функцией: s = υt. При этом, чем круче проходит график, то есть чем больше его угол наклона к оси времени, тем больше скорость движения тела.
Мы обсудили самый простой и очень редко встречающийся тип движения — равномерное прямолинейное. На практике большинство движений в природе и технике являются неравномерными.
Неравномерным называется такое движение, при котором скорость тела изменяется с течением времени, и за одинаковые промежутки времени тело проходит различные пути.
Тем не менее, никто не удивится, если вы скажете, что ехали на машине со скоростью 70 км/ч, даже несмотря на то, что по дороге приходилось притормаживать, останавливаться на светофорах и снова разгоняться. Так какую же скорость мы имеем в виду?
Чтобы охарактеризовать неравномерное движение, вводится понятие средней скорости. Она рассчитывается точно так же, как и скорость при равномерном движении: весь пройденный телом путь делится на общее время движения, включая все остановки:

Среднюю скорость можно рассчитать по формуле:

Рассчитанное таким образом значение отражает среднюю скорость движения тела на всём протяжении пути и может отличаться от значений скорости в разные моменты времени.
Если известна средняя скорость движения тела и время его движения, то можно рассчитать пройденное расстояние:
s = υсрt.
В случае, когда известны средняя скорость и пройденный путь, возможно определить время, затраченное на движение:

Графики неравномерного движения отличаются от тех, которые описывают прямолинейное равномерное движение, поскольку первые могут принимать самые разные формы в зависимости от условий задачи.

Например, рассмотрим ситуацию, где велосипедист едет из одного города в другой. Сначала он проезжает 7 километров за 30 мин. Затем делает перерыв на 10 минут. После чего проезжает ещё 8 километров за 40 минут. А последние 3 километра идёт пешком в течение 30 мин. Если предположить, что в каждом временном интервале скорость велосипедиста оставалась постоянной, то графики зависимости пути и скорости от времени будут выглядеть так, как показано на экране.

Среди различных типов неравномерного движения в школе изучают самое простое — прямолинейное равноускоренное (или равнопеременное) движение. Это такой вид движения, при котором скорость тела за одинаковые промежутки времени изменяется на одинаковую величину, а траектория движения представляет собой прямую линию.
Чтобы охарактеризовать, насколько быстро происходит изменение скорости, в физике была введена специальная величина — ускорение. Ускорение показывает, на сколько изменилась скорость тела за определённый промежуток времени. Оно определяется как отношение изменения скорости ко времени, за которое это изменение произошло:

Ускорение обозначается малой латинской буквой «а». Тогда формула для определения ускорения будет иметь вид, показанный на экране:

Здесь υ0 — это начальная скорость тела, а υ — конечная.
Безусловно, ускорение, подобно скорости, является векторной величиной. А направление вектора ускорения совпадает с направлением вектора изменения скорости тела.
Ускорение может быть как положительным, так и отрицательным. Если начальная скорость тела меньше конечной, то при расчёте ускорения положительное число делится на положительное, и результат будет положительным. Это означает, что тело разгоняется.
Если же тело замедляется, то начальная скорость окажется больше конечной, разница скоростей станет отрицательной. И ускорение также будет отрицательным.
В Международной системе единиц (СИ) единицей ускорения считается такое равноускоренное движение, при котором скорость тела за каждую секунду увеличивается на один метр в секунду. Эту единицу называют «метр на секунду в квадрате» и обозначают: м/с².
Интересно, что в античной механике не существовало чёткой математической формулировки скорости. До XVII века учёные не пользовались понятием скорости таким, каким оно известно сегодня. Несмотря на умение измерять расстояния и время, деление этих разнородных величин считалось лишённым смысла. Аналогично тому, как бессмысленно было бы сравнивать, скажем, расстояние и массу.
Конец XVI века ознаменовался появлением первого устройства для измерения скорости движения кораблей, известного под названием «лаг».

Устройство состояло из деревянной доски с прикреплённым к ней грузом и верёвки, на которой через равные промежутки (около 15,5 метров) были завязаны узлы. Время измеряли с помощью песочных часов, рассчитанных на 30 секунд. Доску опускали в воду, а корабль двигался вперёд. Во время этого процесса верёвка постепенно разматывалась, и моряки считали количество узлов, ушедших за борт, пока песок пересыпался в часах. Именно этот метод измерения стал основой для появления термина «узел» в мореплавании и авиации.
Для измерения скорости транспортного средства на суше используется прибор, называемый спидометром. Первый автомобильный спидометр появился в 1901 году. Однако настоящий прорыв в этой области произошёл спустя 15 лет благодаря изобретателю Николе Тесле. Он запатентовал модель спидометра, принципы работы которой используются и в современных автомобилях.

Для измерения и контроля скорости транспортных средств на дорогах широко применяются радарные системы.
Для измерения скорости и направления ветра применяется прибор, называемый анемометром. Он часто применяется метеорологами для изучения погодных явлений.

А также учёными-физиками, исследующими движение воздушных масс и газов. Простой анемометр состоит из трёх или четырёх чашечек, закреплённых на вертикальной оси. Когда ветер воздействует на чашечки, они начинают вращаться, передавая вращательное движение оси. Скорость ветра рассчитывается исходя из количества оборотов, сделанных чашечками за определённое время.
По схожему принципу работает прибор, известный как вертушка, который предназначен для измерения скорости течения воды в реках и каналах.

 Получите свидетельство
Получите свидетельство Вход
Вход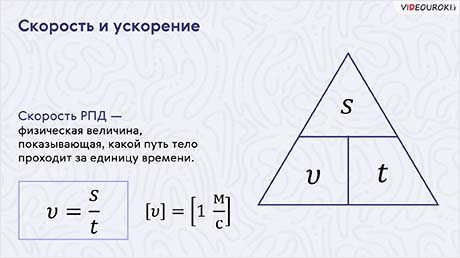




 1595
1595

