Зеркальная симметрия

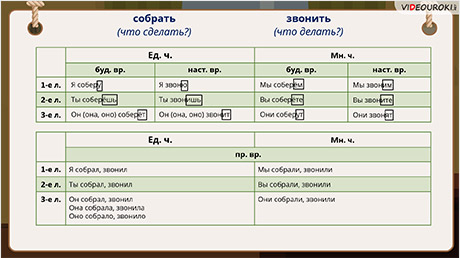
Сегодня на уроке мы вспомним такое понятие, как зеркальная симметрия или симметрия относительно плоскости, проверим, будет ли зеркальная симметрия движением пространства.

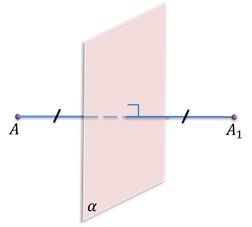
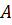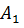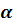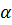Точки  и называются симметричными относительно плоскости , если плоскость  проходит через середину отрезка 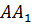 и перпендикулярна к этому отрезку.

Плоскость 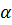 называется плоскостью симметрии.

Каждая точка плоскости 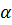 считается симметричной самой себе.

Сформулируем ещё одно определение зеркальной симметрии.

Зеркальной симметрией или симметрией относительно плоскости 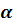 называется такое отображение пространства на себя, при котором любая точка 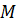 переходит в симметричную ей относительно плоскости 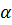 точку .

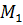Теперь давайте попробуем определить, будет ли зеркальная симметрия являться движением пространства.

Введём прямоугольную систему координат Оxyz так, чтобы плоскость Оxy совпала с плоскостью симметрии и попробуем установить связь между координатами двух точек: точки М с координатами x, y, z и точки М₁ с координатами x₁, y₁,z₁ симметричных относительно плоскости Оxy.

Тогда, если точка М не лежит в плоскости Оxy, то эта плоскость проходит через середину отрезка ММ₁ и перпендикулярна к нему. Из того, что плоскость проходит через середину отрезка ММ₁ можно записать, что точка пересечения прямой и плоскости имеет аппликатой полусумму аппликат точек М и М₁. Поскольку это координатная плоскость, то аппликаты всех точек плоскости равны нулю. Тогда получаем, что аппликата точки М₁ равна – z. Поскольку ось Оxy перпендикулярна отрезку ММ₁, то, значит, этот отрезок параллелен оси Оz, и, следовательно, x₁ = x, y₁ = y.

Если же точка М лежит в плоскости Оxy, то она по определению плоскости симметрии отображается сама на себя. Аппликаты точек плоскости Оxy равны нулю, то есть выполняется условие, что z₁ = – z. Также очевидно выполнение равенств x₁ = x и y₁ = y.

Если в качестве плоскости симметрии взять координатную плоскость Оxz, то для координат точки симметричной точке М, будут справедливы равенства x₁ = – x, y₁ = y, z₁ = z.

Если в качестве плоскости симметрии взять координатную плоскость Оyz, то для координат точки симметричной точке М, будут справедливы равенства x₁ = x, y₁ = – y, z₁ = z.

Теперь давайте рассмотрим две произвольные точки:  и . Построим симметричные им точки , , выбрав в качестве плоскости симметрии плоскость Оxy. По только что доказанным формулам, координаты точки .

Координаты точки . Запишем формулу для вычисления расстояний  и .

Получим одинаковые выражения, то есть , то есть при зеркальной симметрии сохраняется расстояние между точками, значит, зеркальная симметрия – движение пространства.

Задача: найти координаты точек, в которые переходят точки , ,  при зеркальной симметрии относительно координатных плоскостей.

Решение: применим только что полученные формулы. Тогда получим,

Если точка  симметрична точке  относительно плоскости  то справедливы формулы: .

Точка  .

Точка  .

Точка  .

Если точка  симметрична точке  относительно плоскости  то справедливы формулы: .

Точка  .

Точка  .

Точка  .

Если точка  симметрична точке  относительно оси  то справедливы формулы: .

Точка  .

Точка  .

Точка  .

Итоги:

Сегодня на уроке мы вспомнили такое понятие как зеркальная симметрия или симметрия относительно плоскости, доказали, что зеркальная симметрия является движением пространства. Применили полученные знания для решения задачи.