Свойства среднего арифметического

Сегодня на занятии мы познакомимся со свойствами среднего арифметического.

Напомним, что средним арифметическим числового массива называется отношение суммы всех чисел массива к их количеству. Также можно сказать, что среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а в знаменателе – их количество.

Как вы уже знаете, иногда среднее арифметическое называют просто средним, или средним значением.

Среднее арифметическое хорошо описывает однородные массивы данных, то есть массивы, в которых величины имеют один и тот же смысл, и нет значений, которые сильно отличаются от большинства. Иногда среднее арифметическое используют для описания данных в силу сложившейся традиции.

Среднее арифметическое чисел набора принято обозначать .

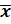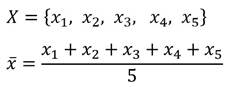
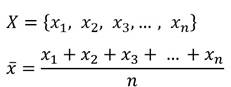
Буквенные обозначения позволяют записать и доказать свойства среднего арифметического числового массива.

Свойство первое. Если каждое число набора увеличить (уменьшить) на одно и то же число , то среднее арифметическое набора увеличится (уменьшится) на это же число .

Докажем свойство на примере массива из 5 чисел.

Свойство второе. Если каждое число набора умножить на одно и то же число , то среднее арифметическое набора также умножится на число .

Докажем свойство на примере массива из 5 чисел.

Выполним несколько заданий.

Задание первое. Среднее арифметическое числового  равно 7. Найдите среднее арифметическое числового набора, который получится, если к каждому числу данного набора прибавить число 5.

Решение. У нас есть набор, среднее арифметическое которого равно 7.

Мы знаем, что если каждое число набора увеличить (уменьшить) на одно и то же число , то среднее арифметическое набора увеличится (уменьшится) на это же число .

Тогда, если к каждому числу данного набора прибавить число 5, то среднее арифметическое набора, который получится, будет равно сумме 7 и 5, то есть 12.

Задание второе. Среднее арифметическое числового набора  равно 11. Найдите среднее арифметическое числового набора, который получится, если каждое число данного набора умножить на число –4

Решение. Есть числовой набор, среднее арифметическое которого равно 11.

Мы доказали, что если каждое число набора умножить на одно и то же число , то среднее арифметическое набора также умножится на число.

Тогда если каждое число данного набора умножить на число –4, то среднее арифметическое набора, который получится, будет равно произведению 11 и –4, то есть –44.

Задание третье. Среднее арифметическое числового набора  равно 10. Сначала к каждому числу этого набора прибавили число 3, а затем каждое полученное число умножили на 2. Найдите среднее арифметическое получившегося числового набора.

Решение. Дан числовой набор, среднее арифметическое которого равно 10.

Прибавив к каждому числу данного набора число 3, получим числовой набор, среднее арифметическое которого равно сумме 10 и 3, то есть 13. Затем, умножив каждое число полученного числового набора на 2, получим новый числовой набор, среднее арифметическое которого равно произведению 13 и 2, то есть 26.

До встречи на следующих занятиях!